
【题目】【2017安徽淮南二模】随着社会发展,淮北市在一天的上下班时段也出现了堵车严重的现象.交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念.记交通指数为T,其范围为[0,10],分别有5个级别:T∈[0,2)畅通;T∈[2,4)基本畅通;T∈[4,6)轻度拥堵;T∈[6,8)中度拥堵;T∈[8,10]严重拥堵.早高峰时段(T≥3 ),从淮北市交通指挥中心随机选取了一至四马路之间50个交通路段,依据交通指数数据绘制的直方图如图所示:
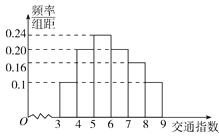
(I)据此直方图估算交通指数T∈[4,8)时的中位数和平均数;
(II)据此直方图求出早高峰一至四马路之间的3个路段至少有2个严重拥堵的概率是多少?
(III)某人上班路上所用时间若畅通时为20分钟,基本畅通为30分钟,轻度拥堵为35分钟,中度拥堵为45分钟,严重拥堵为60分钟,求此人用时间的数学期望.
【答案】(1)4.72.(2)![]() (3)40.6
(3)40.6
【解析】试题分析:(1)由直方图可得,根据中位数的计算公式可求得中位数,利用频率直方图,可计算交通指数的平均数.
(2)设事件![]() 为“1条路段严重拥堵”,得
为“1条路段严重拥堵”,得![]() ,则
,则![]() 条路段中至少有
条路段中至少有![]() 条路段严重拥堵的概率.
条路段严重拥堵的概率.
(3)由题意,得到时间X的分布列,利用期望的公式,即可求解数学期望,得到结论.
试题解析:
(1)由直方图知:T∈[4,8)时交通指数的中位数在T∈[5,6),且为 5+1×![]() =
=![]()
T∈[4,8)时交通指数的平均数为:
4.5×0.2+5.5×0.24+6.5×0.2+7.5×0.16=4.72.
(2)设事件A为“1条路段严重拥堵”,则P(A)=0.1,
则3条路段中至少有2条路段严重拥堵的概率为:
P=C32×(![]() )2×(1-
)2×(1-![]() )+C33×(
)+C33×(![]() )3=
)3=![]() ,
,
所以3条路段中至少有2条路段严重拥堵的概率为![]() .
.
(3)由题意,所用时间X的分布列如下表:
X | 30 | 35 | 45 | 60 |
P | 0.1 | 0.44 | 0.36 | 0.1 |
则E(X)=30×0.1+35×0.44+45×0.36+60×0.1=40.6,
所以此人上班路上所用时间的数学期望是40.6分钟.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】某媒体为了解某地区大学生晚上放学后使用手机上网情况,随机抽取了100名大学生进行调查.如图是根据调查结果绘制的学生每晚使用手机上网平均所用时间的频率分布直方图.将时间不低于40分钟的学生称为“手机迷”. 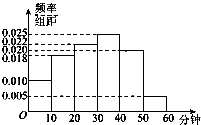
(1)样本中“手机迷”有多少人?
(2)根据已知条件完成下面的2×2列联表,并据此资料判断是否有95%的把握认为“手机迷”与性别有关?
(3)将上述调查所得到的频率视为概率.现在从该地区大量大学 生中,采用随机抽样方法每次抽取1名大学生,抽取3次,经调查一名“手机迷”比“非手机迷”每月的话费平均多40元,记被抽取的3名大学生中的“手机迷”人数为X,且设3人每月的总话费比“非手机迷”共多出Y元,若每次抽取的结果是相互独立的,求X的分布列和Y的期望EY
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和Sn满足2Sn=3an﹣3,数列{bn}的前n项和Tn满足 ![]() =
= ![]() +1且b1=1.
+1且b1=1.
(1)求数列{an},{bn}的通项公式;
(2)设cn= ![]() ,求数列{cn}的前n项和Pn;
,求数列{cn}的前n项和Pn;
(3)数列{Sn}中是否存在不同的三项Sp , Sq , Sr , 使这三项恰好构成等差数列?若存在,求出p,q,r的关系;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】极坐标系的极点为直角坐标系的原点,极轴为x轴的正半轴,两种坐标系中的长度单位相同,已知曲线C的极坐标方程为ρ=2(cosθ+sinθ).
(1)求C的直角坐标方程;
(2)直线l: 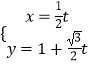 为参数)与曲线C交于A,B两点,与y轴交于E,求|EA|+|EB|的值.
为参数)与曲线C交于A,B两点,与y轴交于E,求|EA|+|EB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线 ![]() x+y﹣
x+y﹣ ![]() =0经过椭圆C:
=0经过椭圆C: ![]() +
+ ![]() =1(a>b>0)的右焦点和上顶点.
=1(a>b>0)的右焦点和上顶点.
(1)求椭圆C的标准方程;
(2)过点(0,﹣2)的直线l与椭圆C交于不同的A,B两点,若∠AOB为钝角,求直线l的斜率k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017重庆二诊】“微信运动”已成为当下热门的健身方式,小王的微信朋友圈内也有大量好友参与了“微信运动”,他随机选取了其中的40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下:
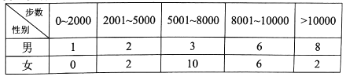
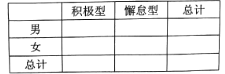
(1)已知某人一天的走路步数超过8000步被系统评定“积极型”,否则为“懈怠型”,根据题意完成下面的![]() 列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
附: 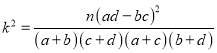 ,
,
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
(2)若小王以这40位好友该日走路步数的频率分布来估计其所有微信好友每日走路步数的概率分布,现从小王的所有微信好友中任选2人,其中每日走路不超过5000步的有![]() 人,超过10000步的有
人,超过10000步的有![]() 人,设
人,设![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】双曲线 ![]() =1(a>0,b>0)的左右焦点分别为F1 , F2渐近线分别为l1 , l2 , 位于第一象限的点P在l1上,若l2⊥PF1 , l2∥PF2 , 则双曲线的离心率是( )
=1(a>0,b>0)的左右焦点分别为F1 , F2渐近线分别为l1 , l2 , 位于第一象限的点P在l1上,若l2⊥PF1 , l2∥PF2 , 则双曲线的离心率是( )
A.![]()
B.![]()
C.2
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司过去五个月的广告费支出x与销售额y(单位:万元)之间有下列对应数据:
x | 2 | 4 | 5 | 6 | 8 |
y |
| 40 | 60 | 50 | 70 |
工作人员不慎将表格中y的第一个数据丢失.已知y对x呈线性相关关系,且回归方程为 ![]() =6.5x+17.5,则下列说法:
=6.5x+17.5,则下列说法:
①销售额y与广告费支出x正相关;
②丢失的数据(表中 ![]() 处)为30;
处)为30;
③该公司广告费支出每增加1万元,销售额一定增加6.5万元;
④若该公司下月广告投入8万元,则销售额为70万元.
其中,正确说法有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com