
【题目】若正实数a,b满足a+b=1,则( )
A.![]() 有最大值4
有最大值4
B.ab有最小值 ![]()
C.![]() 有最大值
有最大值 ![]()
D.a2+b2有最小值 ![]()
【答案】C
【解析】解:∵正实数a,b满足a+b=1,
∴ ![]() =
= ![]() =2+
=2+ ![]() ≥2+2=4,故
≥2+2=4,故 ![]() 有最小值4,故A不正确.
有最小值4,故A不正确.
由基本不等式可得 a+b=1≥2 ![]() ,∴ab≤
,∴ab≤ ![]() ,故ab有最大值
,故ab有最大值 ![]() ,故B不正确.
,故B不正确.
由于 ![]() =a+b+2
=a+b+2 ![]() =1+2
=1+2 ![]() ≤2,∴
≤2,∴ ![]() ≤
≤ ![]() ,故
,故 ![]() 有最大值为
有最大值为 ![]() ,故C正确.
,故C正确.
∵a2+b2 =(a+b)2﹣2ab=1﹣2ab≥1﹣ ![]() =
= ![]() ,故a2+b2有最小值
,故a2+b2有最小值 ![]() ,故D不正确.
,故D不正确.
故选:C.
由于 ![]() =
= ![]() =2+
=2+ ![]() ≥4,故A不正确.
≥4,故A不正确.
由基本不等式可得 a+b=1≥2 ![]() ,可得 ab≤
,可得 ab≤ ![]() ,故B不正确.
,故B不正确.
由于 ![]() =1+2
=1+2 ![]() ≤2,故
≤2,故 ![]() ≤
≤ ![]() ,故 C 正确.
,故 C 正确.
由a2+b2 =(a+b)2﹣2ab≥1﹣ ![]() =
= ![]() ,故D不正确.
,故D不正确.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】葫芦岛市交通局为了解机动车驾驶员对交通法规的知晓情况,对渤海、丰乐、安宁、天正四个社区做分层抽样调查.其中渤海社区有驾驶员96人.若在渤海、丰乐、安宁、天正四个社区抽取驾驶员的人数分别为12,21,25,43,则丰乐、安宁、天正三个社区驾驶员人数是多少( )
A.101
B.808
C.712
D.89
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学高三年级从甲、乙两个班级各选出8名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图所示,其中甲班学生成绩的平均分是86,乙班学生成绩的中位数是83,则 ![]() 的值为( )
的值为( )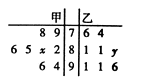
A.9
B.10
C.11
D.13
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位实行休年假制度三年以来,50名职工休年假的次数进行的调查统计结果如表所示:
根据下表信息解答以下问题:
休假次数 | 0 | 1 | 2 | 3 |
人数 | 5 | 10 | 20 | 15 |
(1)从该单位任选两名职工,用η表示这两人休年假次数之和,记“函数f(x)=x2﹣ηx﹣1在区间(4,6)上有且只有一个零点”为事件A,求事件A发生的概率P;
(2)从该单位任选两名职工,用ξ表示这两人休年假次数之差的绝对值,求随机变量ξ的分布列及数学期望Eξ.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】f(x),g(x)分别是定义在R上的奇函数和偶函数,当x<0时,f′(x)g(x)+f(x)g′(x)>0,且g(﹣3)=0,则不等式f(x)g(x)<0的解集是( )
A.(﹣∞,﹣3)∪(0,3)
B.(﹣∞,﹣3)∪(3,+∞)
C.(﹣3,0)∪(3,+∞)
D.(﹣3,0)∪(0,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,侧棱AA1⊥底面ABC,底面ABC等边三角形,E,F分别是BC,CC1的中点.求证: (Ⅰ) EF∥平面A1BC1;
(Ⅱ) 平面AEF⊥平面BCC1B1 . 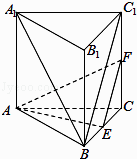
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com