
 ,
, ,给出下列相关命题:①
,给出下列相关命题:① ;②直线MN的方程为3x+10y-28=0;③直线MN必过△ABC的外心;④向量
;②直线MN的方程为3x+10y-28=0;③直线MN必过△ABC的外心;④向量 所在射线必过N点,上述四个命题中正确的是 .(将正确的选项全填上).
所在射线必过N点,上述四个命题中正确的是 .(将正确的选项全填上).  ).N(
).N( ).由此能够得到
).由此能够得到 与
与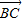 不平行;直线MN的方程为3x+10y-28=0;直线MN不过△ABC的外心;向量
不平行;直线MN的方程为3x+10y-28=0;直线MN不过△ABC的外心;向量 所在射线不一定过N点.
所在射线不一定过N点. ,
, ,
, ,
, ,
, ,
, ,
, =(1-x,
=(1-x, ),
), ).
). ,
, )=
)= (8-3x,6-3y)=(
(8-3x,6-3y)=( ,2-y),
,2-y), ).
). ,
, ,
, =-3≠0,
=-3≠0, 与
与 不平行,
不平行, ),N(
),N( ),
), ,
, ,线段AB的中点(1,
,线段AB的中点(1, ),kAC=0,线段AC的中点(3,1),
),kAC=0,线段AC的中点(3,1), =-
=- ,即4x+6y-19=0,
,即4x+6y-19=0, ,得△ABC的外心为(3,
,得△ABC的外心为(3, ),
), )代入3x+10y-28=0,不成立,
)代入3x+10y-28=0,不成立, )=λ[(2,3)+(6,0)]=λ(8,3)=(8λ,3λ),
)=λ[(2,3)+(6,0)]=λ(8,3)=(8λ,3λ), 所在射线不一定过N点,故④不正确.
所在射线不一定过N点,故④不正确.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| m |
| A |
| 2 |
| A |
| 2 |
| n |
| A |
| 2 |
| A |
| 2 |
| m |
| n |
| 1 |
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| (AB)2 |
| AB |
| AC |
| BA |
| BC |
| CA |
| CB |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com