
【题目】某快递公司收取快递费用的标准是:重量不超过![]() 的包裹收费
的包裹收费![]() 元;重量超过
元;重量超过![]() 的包裹,除
的包裹,除![]() 收费
收费![]() 元之外,超过
元之外,超过![]() 的部分,每超出
的部分,每超出![]() (不足
(不足![]() 时按
时按![]() 计算)需再收
计算)需再收![]() 元.公司从承揽过的包裹中,随机抽取
元.公司从承揽过的包裹中,随机抽取![]() 件,其重量统计如下:
件,其重量统计如下:

公司又随机抽取了![]() 天的揽件数,得到频数分布表如下:
天的揽件数,得到频数分布表如下:

以记录的![]() 天的揽件数的频率作为各揽件数发生的概率
天的揽件数的频率作为各揽件数发生的概率
![]() 计算该公司
计算该公司![]() 天中恰有
天中恰有![]() 天揽件数在
天揽件数在![]() 的概率;
的概率;
![]() 估计该公司对每件包裹收取的快递费的平均值;
估计该公司对每件包裹收取的快递费的平均值;
![]() 公司将快递费的三分之一作为前台工作人员的工资和公司利润,剩余的用做其他费用,目前前台有工作人员
公司将快递费的三分之一作为前台工作人员的工资和公司利润,剩余的用做其他费用,目前前台有工作人员![]() 人,每人每天揽件不超过
人,每人每天揽件不超过![]() 件,每人每天工资
件,每人每天工资![]() 元,公司正在考虑是否将前台工作人员裁减
元,公司正在考虑是否将前台工作人员裁减![]() 人,试计算裁员前后公司每日利润的数学期望,并判断裁员是否对提高公司利润有利?(同一组中的揽件数以这组数据所在区间中点值作代表)
人,试计算裁员前后公司每日利润的数学期望,并判断裁员是否对提高公司利润有利?(同一组中的揽件数以这组数据所在区间中点值作代表)
【答案】(1)![]() ; (2)该公司对每件快递收取的费用的平均值可估计为
; (2)该公司对每件快递收取的费用的平均值可估计为![]() 元;(3)公司将前台工作人员裁员
元;(3)公司将前台工作人员裁员![]() 人对提高公司利润不利.
人对提高公司利润不利.
【解析】
![]() 样本中包裹件数在
样本中包裹件数在![]() 内的天数为
内的天数为![]() ,频率为
,频率为![]() ,可估计概率为
,可估计概率为![]() ,未来
,未来![]() 天中包裹件数在
天中包裹件数在![]() 间的天数
间的天数![]() ,故所求概率为
,故所求概率为![]() ;(2)
;(2)
先列出样本中快递费用及包裹件数表,再利用平均数的公式求快递费的平均值;(3)先求出若不裁员,公司平均每日利润的期望值为![]() (元),再求出若裁减
(元),再求出若裁减![]() 人,公司平均每日利润的期望值为
人,公司平均每日利润的期望值为![]() (元),因
(元),因![]() 故公司将前台工作人员裁员
故公司将前台工作人员裁员![]() 人对提高公司利润不利.
人对提高公司利润不利.
![]() 样本中包裹件数在
样本中包裹件数在![]() 内的天数为
内的天数为![]() ,频率为
,频率为![]() ,
,
可估计概率为![]() ,未来
,未来![]() 天中,包裹件数在
天中,包裹件数在![]() 间的天数X服从二项分布,
间的天数X服从二项分布,
即![]() ,故所求概率为
,故所求概率为![]() ;
;
![]() 样本中快递费用及包裹件数如下表:
样本中快递费用及包裹件数如下表:
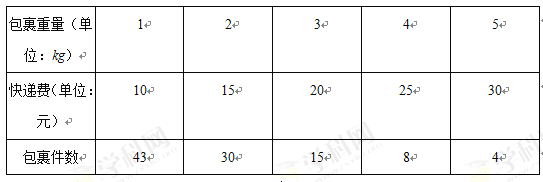
故样本中每件快递收取的费用的平均值为![]() (元),
(元),
故该公司对每件快递收取的费用的平均值可估计为![]() 元.
元.
(3)根据题意及![]() ,揽件数每增加
,揽件数每增加![]() ,可使前台工资和公司利润增加
,可使前台工资和公司利润增加![]() (元),
(元),
将题目中的天数转化为频率,得
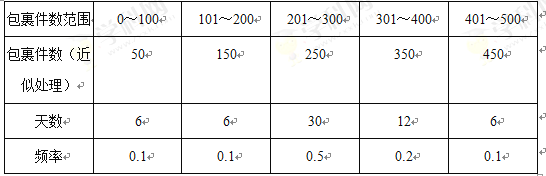
若不裁员,则每天可揽件的上限为![]() 件,公司每日揽件数情况如下:
件,公司每日揽件数情况如下:
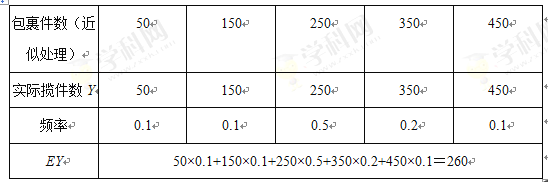
故公司平均每日利润的期望值为![]() (元);
(元);
若裁员![]() 人,则每天可揽件的上限为
人,则每天可揽件的上限为![]() 件,公司每日揽件数情况如下:
件,公司每日揽件数情况如下:

故公司平均每日利润的期望值为![]() (元)
(元)
因![]() 故公司将前台工作人员裁员
故公司将前台工作人员裁员![]() 人对提高公司利润不利.
人对提高公司利润不利.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:
【题目】有下列说法:
①一支田径队有男女运动员98人,其中男运动员有56人.按男、女比例用分层抽样的方法,从全体运动员中抽出一个容量为28的样本,那么应抽取女运动员人数是12人;
②在某项测量中,测量结果X服从正态分布N(1,σ2)(σ>0),若X在(0,1)内取值的概率为0.4,则X在(0,2)内取值的概率为0.8.
③废品率x%和每吨生铁成本y(元)之间的回归直线方程为![]() 2x+256,这表明废品率每增加1%,生铁成本大约增加258元;
2x+256,这表明废品率每增加1%,生铁成本大约增加258元;
④为了检验某种血清预防感冒的作用,把500名未使用血清和使用血清的人一年中的感冒记录作比较,提出假设H0:“这种血清不能起到预防作用”,利用2×2列联表计算得K2的观测值k≈3.918,经查对临界值表知P(K2≥3841)≈0.05,由此,得出以下判断:在犯错误的概率不超过0.05的前提下认为“这种血清能起到预防的作用”,
正确的有( )
A.①②④B.①②③C.①③D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表是![]() 年
年![]() 个重点城市(序号
个重点城市(序号![]() 为一线城市,其它为非一线城市)的月平均收入与房价对照表,根据表中数据并适当修正,得到房价中位数与月平均收入的线性回归方程是
为一线城市,其它为非一线城市)的月平均收入与房价对照表,根据表中数据并适当修正,得到房价中位数与月平均收入的线性回归方程是![]() ,我们把根据房价与月平均收入的线性回归方程得到的房价称为参考房价,若实际房价中位数大于参考房价,我们称这个城市是“房价偏贵城市”.
,我们把根据房价与月平均收入的线性回归方程得到的房价称为参考房价,若实际房价中位数大于参考房价,我们称这个城市是“房价偏贵城市”.
序号 | 月评价收入 | 房价中位数 | 参考房价 | 序号 | 月评价收入 | 房价中位数 | 参考房价 | 序号 | 月评价收入 | 房价中位数 | 参考房价 |
1 | 10670 | 67822 | 11 | 7081 | 17327 | 25704 | 21 | 7081 | 14792 | 15972 | |
2 | 10015 | 52584 | 51180 | 12 | 7065 | 13918 | 19476 | 22 | 7065 | 18741 | 15780 |
3 | 9561 | 50900 | 45732 | 13 | 7027 | 16286 | 19404 | 23 | 7027 | 10538 | 15324 |
4 | 8798 | 30729 | 36576 | 14 | 6974 | 16667 | 18204 | 24 | 6974 | 12069 | 14688 |
5 | 7424 | 10926 | 20088 | 15 | 6920 | 9743 | 17760 | 25 | 6920 | 2333 | 14040 |
6 | 7825 | 26714 | 24900 | 16 | 6903 | 10627 | 18120 | 26 | 6903 | 13582 | 13836 |
7 | 7770 | 39723 | 24240 | 17 | 6884 | 29000 | 17388 | 27 | 6884 | 22126 | 13608 |
8 | 7750 | 15114 | 24000 | 18 | 6654 | 7979 | 16584 | 28 | 6654 | 12207 | 10848 |
9 | 7723 | 17727 | 23676 | 19 | 6648 | 12500 | 16920 | 29 | 6648 | 12472 | 10776 |
10 | 7635 | 13012 | 22620 | 20 | 6608 | 12298 | 16200 | 30 | 6608 | 16406 | 10286 |
(1)计算城市![]() 的参考房价;
的参考房价;
(2)从![]() 个一线城市中随机选取
个一线城市中随机选取![]() 个城市进行调研,求恰好选到一个“房价偏贵城市”的概率;
个城市进行调研,求恰好选到一个“房价偏贵城市”的概率;
(3)完成下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为一线城市与该城市为“房价偏贵城市”有关?
的把握认为一线城市与该城市为“房价偏贵城市”有关?
一般城市 | 非一线城市 | 总计 | |
房价偏贵城市 | |||
不是房价偏贵城市 | |||
总计 |
附参考公式及数据:![]() ,其中
,其中![]() .
.
| 0.100 | 0.050 | 0.01 |
| 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知五边形ABECD有一个直角梯形ABCD与一个等边三角形BCE构成,如图1所示,![]() ,且
,且![]() ,将梯形ABCD沿着BC折起,形成如图2所示的几何体,且
,将梯形ABCD沿着BC折起,形成如图2所示的几何体,且![]() 平面BEC.
平面BEC.
![]() 求证:平面
求证:平面![]() 平面ADE;
平面ADE;
![]() 求二面角
求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
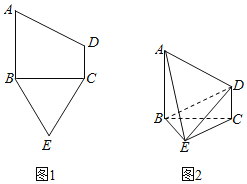
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】双十一购物狂欢节,源于淘宝商城(天猫)![]() 年
年![]() 月
月![]() 日举办的网络促销活动,目前已成为中国电子商务行业的年度盛事,某商家为了解“双十一”这一天网购者在其网店一次性购物情况,从这一天交易成功的所有订单里随机抽取了
日举办的网络促销活动,目前已成为中国电子商务行业的年度盛事,某商家为了解“双十一”这一天网购者在其网店一次性购物情况,从这一天交易成功的所有订单里随机抽取了![]() 份,按购物金额(单位:元)进行统计,得到如下频率分布直方图(同一组中的数据用该组区间的中点值做代表计算).
份,按购物金额(单位:元)进行统计,得到如下频率分布直方图(同一组中的数据用该组区间的中点值做代表计算).
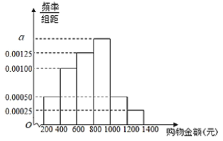
(1)求![]() 的值;
的值;
(2)试估计购物金额的平均数;
(3)若该商家制订了两种不同的促销方案:
方案一:全场商品打八折;
方案二:全场商品优惠如下表:
购物金额范围 |
|
|
|
|
|
|
商家优惠(元) |
|
|
|
|
|
|
如果你是购物者,你认为哪种方案优惠力度更大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 两点分别在
两点分别在![]() 轴和
轴和![]() 轴上运动,且
轴上运动,且![]() ,若动点
,若动点![]() 满足
满足![]() .
.
(1)求出动点P的轨迹对应曲线C的标准方程;
(2)一条纵截距为2的直线![]() 与曲线C交于P,Q两点,若以PQ直径的圆恰过原点,求出直线方程.
与曲线C交于P,Q两点,若以PQ直径的圆恰过原点,求出直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学为了组建一支业余足球队,在高一年级随机选取50名男生测量身高,发现被测男生的身高全部在160cm到184cm之间,将测量结果按如下方式分成六组:第1组![]() ,第2组
,第2组![]() ,...,第6组
,...,第6组![]() ,如图是按上述分组得到的频率分布直方图,以频率近似概率.
,如图是按上述分组得到的频率分布直方图,以频率近似概率.
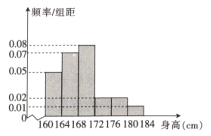
(1)若学校要从中选1名男生担任足球队长,求被选取的男生恰好在第5组或第6组的概率;
(2)现在从第5与第6组男生中选取两名同学担任守门员,求选取的两人中最多有1名男生来自第5组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AB∥CD,∠ABC=90°,AB=1,AC=CD=DA=2,动点M在边DC上(不同于D点),P为边AB上任意一点,沿AM将△ADM翻折成△AD'M,当平面AD'M垂直于平面ABC时,线段PD'长度的最小值为_____.

查看答案和解析>>
科目:高中数学 来源: 题型:
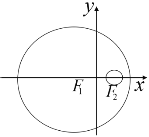
【题目】如图,已知圆![]() 的方程为
的方程为![]() ,圆
,圆![]() 的方程为
的方程为![]() ,若动圆
,若动圆![]() 与圆
与圆![]() 内切,与圆
内切,与圆![]() 外切.
外切.
(Ⅰ)求动圆圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)过直线![]() 上的点
上的点![]() 作圆
作圆![]() 的两条切线,设切点分别是
的两条切线,设切点分别是![]() ,
,![]() ,若直线
,若直线![]() 与轨迹
与轨迹![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com