
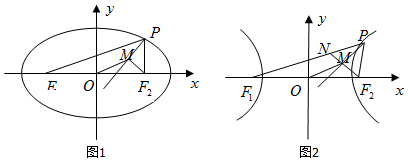
·ÖĪö ĄūÓĆMŹĒ”ĻF1PF2Ę½·ÖĻßÉĻµÄŅ»µć£¬ĒŅF2M”ĶMP£¬ÅŠ¶ĻOMŹĒČż½ĒŠĪF1F2NµÄÖŠĪ»Ļߣ¬°ŃOMÓĆPF1£¬PF2±ķŹ¾£¬ŌŁĄūÓĆĶÖŌ²µÄ½¹°ė¾¶¹«Ź½£¬×Ŗ»ÆĪŖÓĆĶÖŌ²ÉĻµćµÄŗį×ų±ź±ķŹ¾£¬½čÖśĶÖŌ²µÄ·¶Ī§¼“æÉĒó³öOMµÄ·¶Ī§£®
½ā“š 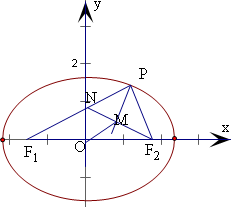 ½ā£ŗČēĶ¼£¬ŃÓ³¤F2M£¬½»PF1ÓėNµć£¬
½ā£ŗČēĶ¼£¬ŃÓ³¤F2M£¬½»PF1ÓėNµć£¬
”ßPMŹĒ”ĻF1PF2Ę½·ÖĻߣ¬ĒŅ$\overrightarrow{{F}_{2}M}$•$\overrightarrow{MP}$=0£¬
ĒŅF2M”ĶMP£¬
”ą|PN|=|PF2|£¬MĪŖF2NµÄÖŠµć£¬
Į¬½ÓOM£¬
”ßOĪŖF1F2ÖŠµć£¬MĪŖF2NÖŠµć£¬
”ą|OM|=$\frac{1}{2}$|F1N|=$\frac{1}{2}$||PF1|-|PN||=$\frac{1}{2}$||PF1|-|PF2||
”ßŌŚĶÖŌ²$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1£Øa£¾b£¾0£©ÖŠ£¬
ÉčPµć×ų±źĪŖ£Øx0£¬y0£©
Ōņ|PF1|=a+ex0£¬|PF2|=a-ex0£¬
”ą||PF1|-|PF2||=|a+ex0-a+ex0|=|2ex0|=2e|x0|=$\frac{2c}{a}$|x0|£¬
¼“ÓŠ|OM|=$\frac{c}{a}$|x0|£¬
”ßPµćŌŚĶÖŌ²$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1£Øa£¾b£¾0£©ÉĻ£¬
”ą|x0|”Ź£Ø0£¬a]£¬
Ó֔ߵ±|x0|=aŹ±£¬F2M”ĶMP²»³ÉĮ¢£¬”ą|x0|”Ź£Ø0£¬a£©£¬
”ą|OM|”Ź£Ø0£¬c£©£®
¹Ź“š°øĪŖ£ŗ£Ø0£¬c£©£®
µćĘĄ ±¾Ģāæ¼²éĮĖĶÖŌ²µÄ¶ØŅ唢±ź×¼·½³Ģ¼°ĘäŠŌÖŹ”¢Čż½ĒŠĪÖŠĪ»Ļß¶ØĄķ£¬æ¼²éĮĖĶĘĄķÄÜĮ¦Óė¼ĘĖćÄÜĮ¦£¬ŹōÓŚÖŠµµĢā£®


 ø÷µŲĘŚÄ©ø“Ļ°ĢŲѵ¾ķĻµĮŠ“š°ø
ø÷µŲĘŚÄ©ø“Ļ°ĢŲѵ¾ķĻµĮŠ“š°ø Š”²©ŹæĘŚÄ©“³¹Ų100·ÖĻµĮŠ“š°ø
Š”²©ŹæĘŚÄ©“³¹Ų100·ÖĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | -$\frac{3}{4}$ | B£® | $\frac{3}{4}$ | C£® | -3 | D£® | 3 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
| ·ÖĄą | »¼ŗōĪüµĄ¼²²” | Ī“»¼ŗōĪüµĄ¼²²” | ŗĻ¼Ę |
| »§Ķā×÷ŅµČĖŌ± | 40 | 60 | 100 |
| ·Ē»§Ķā×÷ŅµČĖŌ± | 60 | 240 | 300 |
| ŗĻ¼Ę | 100 | 300 | 400 |
| P£ØK2”Żk£© | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 0.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
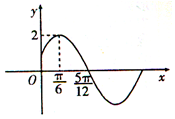 ŅŃÖŖŗÆŹżf£Øx£©=Asin£Ø¦Ųx+¦Õ£©£ØA£¾0£¬¦Ų£¾0£¬$-\frac{¦Š}{2}$£¼¦Õ£¼$\frac{¦Š}{2}$£©µÄ²æ·ÖĶ¼ĻóČēĶ¼ĖłŹ¾£®
ŅŃÖŖŗÆŹżf£Øx£©=Asin£Ø¦Ųx+¦Õ£©£ØA£¾0£¬¦Ų£¾0£¬$-\frac{¦Š}{2}$£¼¦Õ£¼$\frac{¦Š}{2}$£©µÄ²æ·ÖĶ¼ĻóČēĶ¼ĖłŹ¾£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
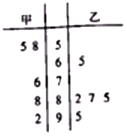 ijŠ£Äā¾Ł°ģ”°³ÉÓļ“óČü”±£¬øßŅ»£Ø1£©°ąµÄ¼×”¢ŅŅĮ½ĆūĶ¬Ń§ŌŚ±¾°ą²Ī¼Ó£ŗ”°³ÉÓļ“óČü”±Ń”°Ī²āŹŌ£¬ŌŚĻąĶ¬µÄ²āŹŌĢõ¼žĻĀ£¬Į½ČĖ5“Ī²āŹŌµÄ³É¼Ø£Øµ„Ī»£ŗ·Ö£©µÄ¾„Ņ¶Ķ¼ČēĶ¼ĖłŹ¾£ŗ
ijŠ£Äā¾Ł°ģ”°³ÉÓļ“óČü”±£¬øßŅ»£Ø1£©°ąµÄ¼×”¢ŅŅĮ½ĆūĶ¬Ń§ŌŚ±¾°ą²Ī¼Ó£ŗ”°³ÉÓļ“óČü”±Ń”°Ī²āŹŌ£¬ŌŚĻąĶ¬µÄ²āŹŌĢõ¼žĻĀ£¬Į½ČĖ5“Ī²āŹŌµÄ³É¼Ø£Øµ„Ī»£ŗ·Ö£©µÄ¾„Ņ¶Ķ¼ČēĶ¼ĖłŹ¾£ŗ²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | £Ø1£¬+”Ž£© | B£® | £Øe£¬+”Ž£© | C£® | £Ø-”Ž£¬-1£© | D£® | £Ø-”Ž£¬-e£© |
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com