
【题目】已知函数f(x)=ax2ex﹣1(a≠0).
(1)求函数f(x)的单调区间;
(2)已知a>0且x∈[1,+∞),若函数f(x)没有零点,求a的取值范围.
【答案】(1)当a>0时,f(x)的单调递增区间为(﹣∞,﹣2)和(0,+∞),单调递减区间为(﹣2,0);当a<0时,f(x)的单调递增区间为(﹣2,0),单调递减区间为(﹣∞,﹣2)和(0,+∞);(2)![]() .
.
【解析】
(1)先求导f'(x)=2axex+ax2ex=axex(2+x),再分a>0和a<0进行讨论即可得解;
(2)根据(1)可知,当a>0时, f(x)在x∈[1,+∞)上单调递增,则保证f(1)>0即可得解.
(1)f'(x)=2axex+ax2ex=axex(2+x),
令f'(x)=0,则x=0或x=﹣2,
①若a>0,
当x<﹣2时,f'(x)>0,f(x)单调递增;
当﹣2<x<0时,f'(x)<0,f(x)单调递减;
当x>0时,f'(x)>0,f(x)单调递增;
②若a<0,
当x<﹣2时,f'(x)<0,f(x)单调递减;
当﹣2<x<0时,f'(x)>0,f(x)单调递增;
当x>0时,f'(x)<0,f(x)单调递减;
综上所述,当a>0时,f(x)的单调递增区间为(﹣∞,﹣2)和(0,+∞),单调递减区间为(﹣2,0);
当a<0时,f(x)的单调递增区间为(﹣2,0),单调递减区间为(﹣∞,﹣2)和(0,+∞).
(2)当a>0时,由(1)可知,f(x)在x∈[1,+∞)上单调递增,
若函数没有零点,则f(1)=ae﹣1>0,解得![]() ,
,
故a的取值范围为![]() .
.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源: 题型:
【题目】2019年在印度尼西亚日惹举办的亚洲乒乓球锦标赛男子团体决赛中,中国队与韩国队相遇,中国队男子选手A,B,C,D,E依次出场比赛,在以往对战韩国选手的比赛中他们五人获胜的概率分别是0.8,0.8,0.8,0.75,0.7,并且比赛胜负相互独立.赛会釆用5局3胜制,先赢3局者获得胜利.
(1)在决赛中,中国队以3∶1获胜的概率是多少?
(2)求比赛局数的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一块半圆形的空地,直径![]() 米,政府计划在空地上建一个形状为等腰梯形的花圃
米,政府计划在空地上建一个形状为等腰梯形的花圃![]() ,如图所示,其中
,如图所示,其中![]() 为圆心,
为圆心,![]() ,
,![]() 在半圆上,其余为绿化部分,设
在半圆上,其余为绿化部分,设![]() .
.
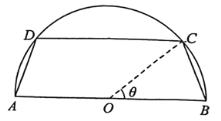
(1)记花圃的面积为![]() ,求
,求![]() 的最大值;
的最大值;
(2)若花圃的造价为10元/米,在花圃的边![]() 、
、![]() 处铺设具有美化效果的灌溉管道,铺设费用为500元/米,两腰
处铺设具有美化效果的灌溉管道,铺设费用为500元/米,两腰![]() 、
、![]() 不铺设,求
不铺设,求![]() 满足什么条件时,会使总造价最大.
满足什么条件时,会使总造价最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代数学名著,它在几何学中的研究比西方早1000多年,在《九章算术》中,将底面为直角三角形,且侧棱垂直于底面的三棱柱称为堑堵(qian du);阳马指底面为矩形,一侧棱垂直于底面的四棱锥,鳖膈(bie nao)指四个面均为直角三角形的四面体.如图在堑堵![]() 中,
中,![]() .
.
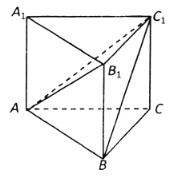
(1)求证:四棱锥![]() 为阳马;
为阳马;
(2)若![]() ,当鳖膈
,当鳖膈![]() 体积最大时,求锐二面角
体积最大时,求锐二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年底,北京2022年冬奥组委会启动志愿者全球招募,仅一个月内报名人数便突破60万,其中青年学生约有50万人.现从这50万青年学生志愿者中,按男女分层抽样随机选取20人进行英语水平测试,所得成绩(单位:分)统计结果用茎叶图记录如下:

(Ⅰ)试估计在这50万青年学生志愿者中,英语测试成绩在80分以上的女生人数;
(Ⅱ)从选出的8名男生中随机抽取2人,记其中测试成绩在70分以上的人数为X,求![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)为便于联络,现将所有的青年学生志愿者随机分成若干组(每组人数不少于5000),并在每组中随机选取![]() 个人作为联络员,要求每组的联络员中至少有1人的英语测试成绩在70分以上的概率大于90%.根据图表中数据,以频率作为概率,给出
个人作为联络员,要求每组的联络员中至少有1人的英语测试成绩在70分以上的概率大于90%.根据图表中数据,以频率作为概率,给出![]() 的最小值.(结论不要求证明)
的最小值.(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一次考试结束后,随机抽查了某校高三(1)班5名同学的数学与物理成绩如下表:
学生 |
|
|
|
|
|
数学 | 89 | 91 | 93 | 95 | 97 |
物理 | 87 | 89 | 89 | 92 | 93 |
(Ⅰ)分别求这5名同学数学与物理成绩的平均分与方差,并估计该班数学与物理成绩那科更稳定;
(Ⅱ)从以上5名同学中选2人参加一项活动,求选中的学生中至少有一个物理成绩高于90分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若曲线![]() 在
在![]() 处的切线与
处的切线与![]() 轴平行,求
轴平行,求![]() ;
;
(2)已知![]() 在
在![]() 上的最大值不小于
上的最大值不小于![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)写出![]() 所有可能的零点个数及相应的
所有可能的零点个数及相应的![]() 的取值范围.(请直接写出结论)
的取值范围.(请直接写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四个命题:
①在回归分析中, ![]() 可以用来刻画回归效果,
可以用来刻画回归效果, ![]() 的值越大,模型的拟合效果越好;
的值越大,模型的拟合效果越好;
②在独立性检验中,随机变量![]() 的值越大,说明两个分类变量有关系的可能性越大;
的值越大,说明两个分类变量有关系的可能性越大;
③在回归方程![]() 中,当解释变量
中,当解释变量![]() 每增加1个单位时,预报变量
每增加1个单位时,预报变量![]() 平均增加1个单位;
平均增加1个单位;
④两个随机变量相关性越弱,则相关系数的绝对值越接近于1;
其中真命题是:
A. ①④ B. ②④ C. ①② D. ②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com