
【题目】△ABC中,A、B、C的对边分别为a,b,c,面积为S,满足S= ![]() (a2+b2﹣c2).
(a2+b2﹣c2).
(1)求C的值;
(2)若a+b=4,求周长的范围与面积S的最大值.
【答案】
(1)解:∵S= ![]() absinC,cosC=
absinC,cosC= ![]() ,
,
即a2+b2﹣c2=2abcosC,
∴S= ![]() (a2+b2﹣c2)变形得:
(a2+b2﹣c2)变形得: ![]() absinC=
absinC= ![]() ×2abcosC,
×2abcosC,
整理得:tanC= ![]() ,
,
又0<C<π,
则C= ![]() ;
;
(2)解:a2+b2﹣c2=2abcosC,可得c2=(a+b)2﹣3ab=16﹣3ab,
由a+b=4≥2 ![]() (当且仅当a=b取等号),
(当且仅当a=b取等号),
即有0<ab≤4,
则c∈[2,4),
则周长的范围是[6,8);
△ABC的面积为S= ![]() absinC=
absinC= ![]() ab≤
ab≤ ![]() ,
,
当且仅当a=b=2,取得最大值 ![]() .
.
【解析】(1)运用三角形的面积公式和余弦定理,结合同角的商数关系,特殊角的三角函数值,可得角C;(2)运用余弦定理和基本不等式,以及三角形的面积公式,可得最大值.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() .
.
(Ⅰ)当![]() 时,求
时,求![]() 在
在![]() 处的切线方程;
处的切线方程;
(Ⅱ)若![]() 且函数
且函数![]() 有且仅有一个零点,求实数
有且仅有一个零点,求实数![]() 的值;
的值;
(Ⅲ)在(Ⅱ)的条件下,若![]() 时,
时, ![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】上世纪八十年代初, 邓小平同志曾指出“在人才的问题上,要特别强调一下,必须打破常规去发现、选拔和培养杰出的人才”. 据此,经省教育厅批准,某中学领导审时度势,果断作出于1985年开始施行超常实验班教学试验的决定.一时间,学生兴奋,教师欣喜,家长欢呼,社会热议.该中学实验班一路走来,可谓风光无限,硕果累累,尤其值得一提的是,1990年,全国共招收150名少年大学生,该中学就有19名实验班学生被录取,占全国的十分之一,轰动海内外.设该中学超常实验班学生第x年被录取少年大学生的人数为y.
左下表为该中学连续5年实验班学生被录取少年大学生人数,求y关于x的线性回归方程,并估计第6年该中学超常实验班学生被录取少年大学生人数;
年份序号x | 1 | 2 | 3 | 4 | 5 |
录取人数y | 10 | 11 | 14 | 16 | 19 |
附1: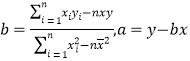
![]()
下表是从该校已经毕业的100名高中生录取少年大学生人数与是否接受超常实验班教育得到
2×2列联表,完成上表,并回答:是否有95%以上的把握认为“录取少年大学生人数与是否接受超常实验班教育有关系”.
附2:
接受超常实验班教育 | 未接受超常实验班教育 | 合计 | |
录取少年大学生 | 60 | 80 | |
未录取少年大学生 | 10 | ||
合计 | 30 | 100 |
![]()
| 0.50 | 0.40 | 0.10 | 005 |
| 0.455 | 0.708 | 2.706 | 3.841 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若方程![]() 所表示的曲线为C,给出下列四个命题:
所表示的曲线为C,给出下列四个命题:
①若C为椭圆,则1<t<4且t≠![]() ;
;
②若C为双曲线,则t>4或t<1;
③曲线C不可能是圆;
④若C表示椭圆,且长轴在x轴上,则1<t<![]() .
.
其中正确的命题是________(把所有正确命题的序号都填在横线上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 是椭圆E:
是椭圆E:![]() (a>b>0)上一点,离心率为
(a>b>0)上一点,离心率为![]() .
.
(1)求椭圆E的方程;
(2)设不过原点O的直线l与该椭圆E交于P,Q两点,满足直线OP,PQ,OQ的斜率依次成等比数列,求△OPQ面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n项和为Sn=n2+pn+q(p,q∈R),且a2 , a3 , a5成等比数列.
(1)求p,q的值;
(2)若数列{bn}满足an+log2n=log2bn , 求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数{an}满a1=0,an+1=an+2n,那a2016的值是( )
A.2014×2015
B.2015×2016
C.2014×2016
D.2015×2015
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两个无穷数列![]() 和
和![]() 的前
的前![]() 项和分别为
项和分别为![]() ,
,![]() ,
,![]() ,
,![]() ,对任意的
,对任意的![]() ,都有
,都有![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)若![]() 为等差数列,对任意的
为等差数列,对任意的![]() ,都有
,都有![]() .证明:
.证明:![]() ;
;
(3)若![]() 为等比数列,
为等比数列,![]() ,
,![]() ,求满足
,求满足![]() 的
的![]() 值.
值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 过圆
过圆![]() 与直线
与直线![]() 的交点,且圆上任意一点关于直线
的交点,且圆上任意一点关于直线![]() 的对称点仍在圆上.
的对称点仍在圆上.
(1)求圆![]() 的标准方程;
的标准方程;
(2)若圆![]() 与
与![]() 轴正半轴的交点为
轴正半轴的交点为![]() ,直线
,直线![]() 与圆
与圆![]() 交于
交于![]() 两点,且点
两点,且点![]() 是
是![]() 的垂线(垂心是三角形三条高线的交点),求直线
的垂线(垂心是三角形三条高线的交点),求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com