
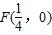 ,直线l:
,直线l: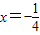 ,点B是l上的动点,若过B垂直于y轴的直线与线段BF的垂直平分线交于点M,则点M的轨迹方程是 .
,点B是l上的动点,若过B垂直于y轴的直线与线段BF的垂直平分线交于点M,则点M的轨迹方程是 .  名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:高中数学 来源: 题型:
| OP |
| OA1 |
| OA2 |
| OP |
| OA1 |
| OA2 |
| OAn |
| OP |
| OA1 |
| OA2 |
| OAn |
| OP |
| OA1 |
| OA2 |
| OAn |
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)已知点A(2,0),B(0,6),O为坐标原点
(1)若点C在线段OB上,且∠BAC=45°,求△ABC的面积.
(2)若原点O关于直线AB的对称点为D,延长BD到P,且|PD|=2|BD|,求P点的坐标。
(3)已知直线L:ax+10y+84-108![]() =0经过P点,求直线L的倾斜角.
=0经过P点,求直线L的倾斜角.
查看答案和解析>>
科目:高中数学 来源:《第2章 圆锥曲线与方程》2010年单元测试卷(4)(解析版) 题型:选择题
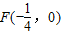 ,直线l:
,直线l: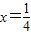 ,点B是直线l上的动点,若过B垂直于y轴的直线与线段BF的垂直平分线交于点M,则点M所在曲线是( )
,点B是直线l上的动点,若过B垂直于y轴的直线与线段BF的垂直平分线交于点M,则点M所在曲线是( )查看答案和解析>>
科目:高中数学 来源:高考数学一轮复习必备(第63课时):第八章 圆锥曲线方程-抛物线(解析版) 题型:选择题
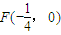 ,直线l:
,直线l: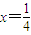 ,点B是直线l上的动点,若过B垂直于y轴的直线与线段BF的垂直平分线交于点M,则点M所在曲线是( )
,点B是直线l上的动点,若过B垂直于y轴的直线与线段BF的垂直平分线交于点M,则点M所在曲线是( )查看答案和解析>>
科目:高中数学 来源:湖北省麻城一中09-10学年高二上学期9月月考(理) 题型:解答题
已知点A(2,0),B(0,6),O为坐标原点
(1)若点C在线段OB上,且∠BAC=45°,求△ABC的面积.
(2)若原点O关于直线AB的对称点为D,延长BD到P,且|PD|=2|BD|,求P点的坐标。
(3)已知直线L:ax+10y+84-108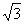 =0经过P点,求直线L的倾斜角.
=0经过P点,求直线L的倾斜角.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com