
【题目】如图,在四棱锥![]() 中,
中,![]() ,
,![]() 分别为
分别为![]() 的中点,
的中点,![]() .
.
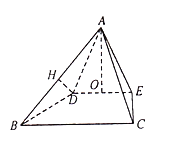
(1)求证:![]() 平面
平面![]() ;
;
(2)求直线![]() 与底面
与底面![]() 所成角的大小
所成角的大小
科目:高中数学 来源: 题型:
【题目】已知直线![]() 与抛物线
与抛物线![]() :
:![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() 的面积为16(
的面积为16(![]() 为坐标原点).
为坐标原点).
(1)求![]() 的方程;
的方程;
(2)直线![]() 经过
经过![]() 的焦点
的焦点![]() 且
且![]() 不与
不与![]() 轴垂直,与
轴垂直,与![]() 交于
交于![]() ,
,![]() 两点,若线段
两点,若线段![]() 的垂直平分线与
的垂直平分线与![]() 轴交于点
轴交于点![]() ,证明:
,证明:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】生男生女都一样,女儿也是传后人.由于某些地区仍然存在封建传统思想,头胎的男女情况可能会影响生二孩的意愿,现随机抽取某地200户家庭进行调查统计.这200户家庭中,头胎为女孩的频率为0.5,生二孩的频率为0.525,其中头胎生女孩且生二孩的家庭数为60.
(1)完成下列![]() 列联表,并判断能否有95%的把握认为是否生二孩与头胎的男女情况有关;
列联表,并判断能否有95%的把握认为是否生二孩与头胎的男女情况有关;
生二孩 | 不生二孩 | 合计 | |
头胎为女孩 | 60 | ||
头胎为男孩 | |||
合计 | 200 |
(2)在抽取的200户家庭的样本中,按照分层抽样的方法在生二孩的家庭中抽取了7户,进一步了解情况,在抽取的7户中再随机抽取4户,求抽到的头胎是女孩的家庭户数![]() 的分布列及数学期望.
的分布列及数学期望.
附:
| 0.15 | 0.05 | 0.01 | 0.001 |
| 2.072 | 3.841 | 6.635 | 10.828 |
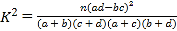 (其中
(其中![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】响应“文化强国建设”号召,某市把社区图书阅览室建设增列为重要的民生工程.为了解市民阅读需求,随机抽取市民200人做调查,统计显示,男士喜欢阅读古典文学的有64人,不喜欢的有56人;女士喜欢阅读古典文学的有36人,不喜欢的有44人.
(1)能否在犯错误的概率不超过0.25的前提下认为喜欢阅读古典文学与性别有关系?
(2)为引导市民积极参与阅读,有关部门牵头举办市读书交流会,从这200人中筛选出5名男代表和4名代表,其中有3名男代表和2名女代表喜欢古典文学.现从这9名代表中任选3名男代表和2名女代表参加交流会,记![]() 为参加交流会的5人中喜欢古典文学的人数,求
为参加交流会的5人中喜欢古典文学的人数,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
附:![]() ,其中
,其中![]() .
.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 、
、![]() 与平面
与平面![]() 、
、![]() 满足
满足![]() ,
,![]() ,
,![]() ,则下列命题中正确的是( )
,则下列命题中正确的是( )
A.![]() 是
是![]() 的充分不必要条件
的充分不必要条件
B.![]() 是
是![]() 的充要条件
的充要条件
C.设![]() ,则
,则![]() 是
是![]() 的必要不充分条件
的必要不充分条件
D.设![]() ,则
,则![]() 是
是![]() 的既不充分也不必要条件
的既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() ,圆
,圆![]() :
:![]() ,直线
,直线![]() :
:![]() 与抛物线
与抛物线![]() 相切于点
相切于点![]() ,且与圆
,且与圆![]() 相切于点
相切于点![]() .
.
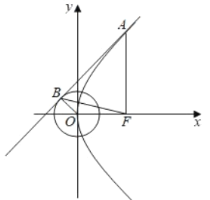
(1)当![]() ,
,![]() 时,求直线
时,求直线![]() 方程与抛物线
方程与抛物线![]() 的方程;
的方程;
(2)设![]() 为抛物线
为抛物线![]() 的焦点,
的焦点,![]() ,
,![]() 的面积分别为
的面积分别为![]() ,
,![]() ,当
,当![]() 取得最大值时,求实数
取得最大值时,求实数![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com