练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    “解方程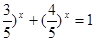（”有如下思路；设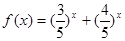，则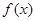在R上单调递减，且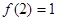，故原方程有唯一解x=2，类比上述解题思路，不等式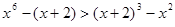的解集是         .

     

    【答案】

    【解析】

    试题分析：根据题意，由于“解方程（”有如下思路；设，则在R上单调递减，且，故原方程有唯一解x=2，那么对于不等式而言，由于，当x=2,x=-1函数值为零，那么并且可以判定函数是先减后增再减的，因此可知满足不等式的解集为

    考点：类比推理

    点评：主要是考查了类比推理的思想的运用，来解不等式，属于中档题。

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知关于x的方程|x2-2x-3|-a=0，该方程实数解的个数有如下判断：
    ①若该方程没有实数根，则a＜-4
    ②若a=0，则该方程恰有两个实数解
    ③该方程不可能有三个不同的实数根
    ④若该方程恰有三个不同的实数解，则a=4
    ⑤若该方程恰有四个不同的实数解，则0＜a＜4
    其中正确判断的序号是
    ②④⑤
    ②④⑤
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    已知关于x的方程|x2-2x-3|-a=0，该方程实数解的个数有如下判断：
    ①若该方程没有实数根，则a＜-4
    ②若a=0，则该方程恰有两个实数解
    ③该方程不可能有三个不同的实数根
    ④若该方程恰有三个不同的实数解，则a=4
    ⑤若该方程恰有四个不同的实数解，则0＜a＜4
    其中正确判断的序号是________．

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年安徽省宣城市宁国中学高一（上）第二次段考数学试卷（解析版） 题型：填空题

    已知关于x的方程|x2-2x-3|-a=0，该方程实数解的个数有如下判断：
    ①若该方程没有实数根，则a＜-4
    ②若a=0，则该方程恰有两个实数解
    ③该方程不可能有三个不同的实数根
    ④若该方程恰有三个不同的实数解，则a=4
    ⑤若该方程恰有四个不同的实数解，则0＜a＜4
    其中正确判断的序号是    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知圆C的方程为有如下两组论断：

               第I组                                     第II组

       （a）点M在圆C内且M不为圆心          （1）直线l与圆C相切

       （b）点M在圆C上                         （2）直线l与圆C相交

       （c）点M在圆C外                          （3）直线l与圆C相离

        把第I组论断作为条件，第II组论断作为结论，写出所有可能成立的命题            .（将命题用序号写成形如的形式）

    查看答案和解析>>

    同步练习册答案