
ЁОЬтФПЁПФГАрЭЌбЇРћгУЙњЧьНкНјааЩчЛсЪЕМљЃЌЖд[25ЃЌ55]ЫъЕФШЫШКЫцЛњГщШЁ![]() ШЫНјааСЫвЛДЮЩњЛюЯАЙпЪЧЗёЗћКЯЕЭЬМЙлФюЕФЕїВщЃЌШєЩњЛюЯАЙпЗћКЯЕЭЬМЙлФюЕФГЦЮЊЁАЕЭЬМзхЁБЃЌЗёдђГЦЮЊЁАЗЧЕЭЬМзхЁБЃЌЕУЕНШчЯТЭГМЦБэКЭИїФъСфЖЮШЫЪ§ЦЕТЪЗжВМжБЗНЭМЃК
ШЫНјааСЫвЛДЮЩњЛюЯАЙпЪЧЗёЗћКЯЕЭЬМЙлФюЕФЕїВщЃЌШєЩњЛюЯАЙпЗћКЯЕЭЬМЙлФюЕФГЦЮЊЁАЕЭЬМзхЁБЃЌЗёдђГЦЮЊЁАЗЧЕЭЬМзхЁБЃЌЕУЕНШчЯТЭГМЦБэКЭИїФъСфЖЮШЫЪ§ЦЕТЪЗжВМжБЗНЭМЃК
зщЪ§ | Зжзщ | ЕЭЬМзхЕФШЫЪ§ | еМБОзщЕФЦЕТЪ |
ЕквЛзщ | [25ЃЌ30) | 120 | 0.6 |
ЕкЖўзщ | [30ЃЌ35) | 195 |
|
ЕкШ§зщ | [35ЃЌ40) | 100 | 0.5 |
ЕкЫФзщ | [40ЃЌ45) |
| 0.4 |
ЕкЮхзщ | [45ЃЌ50) | 30 | 0.3 |
ЕкСљзщ | [50ЃЌ55] | 15 | 0.3 |
(1)ВЙШЋЦЕТЪЗжВМжБЗНЭМВЂЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
(2)ДгФъСфЖЮдк[40ЃЌ50)ЕФЁАЕЭЬМзхЁБжаВЩгУЗжВуГщбљЗЈГщШЁ6ШЫВЮМгЛЇЭтЕЭЬМЬхбщЛюЖЏЃЌЦфжабЁШЁ2ШЫзїЮЊСьЖгЃЌЧѓбЁШЁЕФ2УћСьЖгжаЧЁга1ШЫФъСфдк[40ЃЌ45)ЫъЕФИХТЪ. 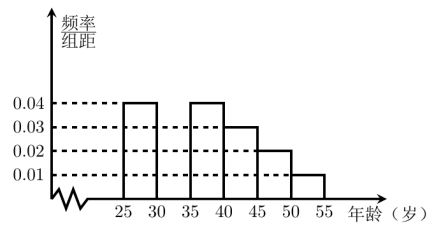
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЈ2ЃЉ
ЃЈ2ЃЉ![]()
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉгЩЬтвтИљОнЦЕТЪЗжВМБэПЩЧѓГіЕквЛзщЕФШЫЪ§ЃЌгЩЙЋЪНЃКЦЕТЪ=ЦЕЪ§/зщЪ§ЃЌдђЕквЛзщЕФШЫЪ§=ЦЕЪ§/ЦЕТЪЃЌдйИљОнЪ§ТЪЗжВМЭМЃЌгЩЕквЛзщЕФзнзјБъДњШыЙЋЪНЃКзнзјБъ=ЦЕТЪ/зщОрЃЌЧѓГіЕквЛзщЕФЦЕТЪЃЌдйгЩЙЋЪНЃКЦЕТЪ=зщЪ§/ШнСПЃЌЧѓГібљБОШнСП![]() ЕФжЕЃЎЭЌРэМДЗжБ№ЫуГі
ЕФжЕЃЎЭЌРэМДЗжБ№ЫуГі![]() гы
гы![]() ЕФжЕЃЛЃЈ2ЃЉгЩЭГМЦБэПЩжЊ[40ЃЌ45ЃЉЫъФъСфЖЮЕФЁАЕЭЬМзхЁБгы[45ЃЌ50ЃЉЫъФъСфЖЮЕФЁАЕЭЬМзхЁБЕФБШжЕЮЊ60ЃК30=2ЃК1ЃЌЫљвдВЩгУЗжВуГщбљЗЈГщШЁ6ШЫЃЌ[40ЃЌ45ЃЉЫъжага4ШЫЃЌ[45ЃЌ50ЃЉЫъжага2ШЫЃЌдйВЩгУСаОйЗЈЃЌИљОнЙХЕфИХаЭЕФМЦЫуЙЋЪНМЦЫуГіЦфИХТЪЃЎ
ЕФжЕЃЛЃЈ2ЃЉгЩЭГМЦБэПЩжЊ[40ЃЌ45ЃЉЫъФъСфЖЮЕФЁАЕЭЬМзхЁБгы[45ЃЌ50ЃЉЫъФъСфЖЮЕФЁАЕЭЬМзхЁБЕФБШжЕЮЊ60ЃК30=2ЃК1ЃЌЫљвдВЩгУЗжВуГщбљЗЈГщШЁ6ШЫЃЌ[40ЃЌ45ЃЉЫъжага4ШЫЃЌ[45ЃЌ50ЃЉЫъжага2ШЫЃЌдйВЩгУСаОйЗЈЃЌИљОнЙХЕфИХаЭЕФМЦЫуЙЋЪНМЦЫуГіЦфИХТЪЃЎ
ЪдЬтНтЮіЃКЃЈЂёЃЉЁпЕкЖўзщЕФЦЕТЪЮЊ1-ЃЈ0ЃЎ04+0ЃЎ04+0ЃЎ03+0ЃЎ02+0ЃЎ01ЃЉЁС5=0ЃЎ3ЃЌ
ЁрИпЮЊ0ЃЎ3![]() 5=0ЃЎ06ЃЎЦЕТЪжБЗНЭМШчЯТЃК
5=0ЃЎ06ЃЎЦЕТЪжБЗНЭМШчЯТЃК
ЕквЛзщЕФШЫЪ§ЮЊ 120![]() 0ЃЎ6=200ЃЌЦЕТЪЮЊ0ЃЎ04ЁС5=0ЃЎ2ЃЌ
0ЃЎ6=200ЃЌЦЕТЪЮЊ0ЃЎ04ЁС5=0ЃЎ2ЃЌ
Ёрn=200![]() 0ЃЎ2=1000ЃЎ
0ЃЎ2=1000ЃЎ
гЩЬтПЩжЊЃЌЕкЖўзщЕФЦЕТЪЮЊ0ЃЎ3ЃЌЁрЕкЖўзщЕФШЫЪ§ЮЊ1000ЁС0ЃЎ3=300ЃЌ
Ёрp=195![]() 300=0ЃЎ65ЃЎ
300=0ЃЎ65ЃЎ
ЕкЫФзщЕФЦЕТЪЮЊ0ЃЎ03ЁС5=0ЃЎ15ЃЌЁрЕкЫФзщЕФШЫЪ§ЮЊ1000ЁС0ЃЎ15=150ЃЌ
Ёрa=150ЁС0ЃЎ4=60ЃЎ
ЃЈЂђЃЉЁп[40ЃЌ45ЃЉЫъФъСфЖЮЕФЁАЕЭЬМзхЁБгы[45ЃЌ50ЃЉЫъФъСфЖЮЕФЁАЕЭЬМзхЁБЕФБШжЕЮЊ60ЃК30=2ЃК1ЃЌЫљвдВЩгУЗжВуГщбљЗЈГщШЁ6ШЫЃЌ[40ЃЌ45ЃЉЫъжага4ШЫЃЌ[45ЃЌ50ЃЉЫъжага2ШЫЃЎ
Щш[40ЃЌ45ЃЉЫъжаЕФ4ШЫЮЊaЁЂbЁЂcЁЂdЃЌ[45ЃЌ50ЃЉЫъжаЕФ2ШЫЮЊmЁЂnЃЌдђбЁШЁ2ШЫзїЮЊСьЖгЕФгаЃЈaЃЌbЃЉЁЂЃЈaЃЌcЃЉЁЂЃЈaЃЌdЃЉЁЂЃЈaЃЌmЃЉЁЂЃЈaЃЌnЃЉЁЂЃЈbЃЌcЃЉЁЂЃЈbЃЌdЃЉЁЂЃЈbЃЌmЃЉЁЂ
ЃЈbЃЌnЃЉЁЂЃЈcЃЌdЃЉЁЂЃЈcЃЌmЃЉЁЂЃЈcЃЌnЃЉЁЂЃЈdЃЌmЃЉЁЂЃЈdЃЌnЃЉЁЂЃЈmЃЌnЃЉЃЌЙВ15жжЃЛ
ЦфжаЧЁга1ШЫФъСфдк[40ЃЌ45ЃЉЫъЕФгаЃЈaЃЌmЃЉЁЂЃЈaЃЌnЃЉЁЂЃЈbЃЌmЃЉЁЂЃЈbЃЌnЃЉЁЂ
ЃЈcЃЌmЃЉЁЂЃЈcЃЌnЃЉЁЂЃЈdЃЌmЃЉЁЂЃЈdЃЌnЃЉЃЌЙВ8жжЃЎ
ЁрбЁШЁЕФ2УћСьЖгжаЧЁга1ШЫФъСфдк[40ЃЌ45ЃЉЫъЕФИХТЪЮЊ![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЕу![]() ЃЌЕу
ЃЌЕу![]() дк
дк![]() жсЩЯЃЌЖЏЕу
жсЩЯЃЌЖЏЕу![]() Тњзу
Тњзу![]() ЃЌЧвжБЯп
ЃЌЧвжБЯп![]() гы
гы![]() жсНЛгк
жсНЛгк![]() ЕуЃЌ
ЕуЃЌ ![]() ЪЧЯпЖЮ
ЪЧЯпЖЮ![]() ЕФжаЕу.
ЕФжаЕу.
ЃЈ1ЃЉЧѓЖЏЕу![]() ЕФЙьМЃ
ЕФЙьМЃ![]() ЕФЗНГЬЃЛ
ЕФЗНГЬЃЛ
ЃЈ2ЃЉШєЕу![]() ЪЧЧњЯп
ЪЧЧњЯп![]() ЕФНЙЕуЃЌЙ§
ЕФНЙЕуЃЌЙ§![]() ЕФСНЬѕжБЯп
ЕФСНЬѕжБЯп![]() ЃЌ
ЃЌ ![]() Йигк
Йигк![]() жсЖдГЦЃЌЧв
жсЖдГЦЃЌЧв![]() НЛЧњЯп
НЛЧњЯп![]() гк
гк![]() ЁЂ
ЁЂ![]() СНЕуЃЌ
СНЕуЃЌ ![]() НЛЧњЯп
НЛЧњЯп![]() гк
гк![]() ЁЂ
ЁЂ![]() СНЕуЃЌ
СНЕуЃЌ ![]() ЁЂ
ЁЂ![]() дкЕквЛЯѓЯоЃЌШєЫФБпаЮ
дкЕквЛЯѓЯоЃЌШєЫФБпаЮ![]() ЕФУцЛ§ЕШгк
ЕФУцЛ§ЕШгк![]() ЃЌЧѓжБЯп
ЃЌЧѓжБЯп![]() ЃЌ
ЃЌ ![]() ЕФЗНГЬ.
ЕФЗНГЬ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
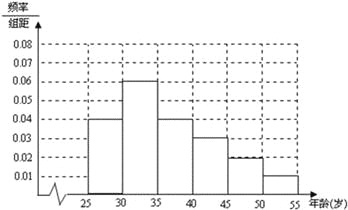
ЁОЬтФПЁПЯждкКмЖрШЫЯВЛЖзджњгЮ,2017ФъаЂИабюЕъЬвЛЈНкЃЌУРРіЕФЬвЛЈЗчОАКЭШЫЮФОАЙлгРДжкЖрБіПЭ.ФГЕїВщЛњЙЙЮЊСЫСЫНтЁАзджњгЮЁБЪЧЗёгыадБ№гаЙиЃЌдкаЂИаЬвЛЈНкЦкМфЃЌЫцЛњГщШЁСЫ![]() ШЫЃЌЕУШчЯТЫљЪОЕФСаСЊБэЃК
ШЫЃЌЕУШчЯТЫљЪОЕФСаСЊБэЃК
доГЩЁАзджњгЮЁБ | ВЛдоГЩЁАзджњгЮЁБ | КЯМЦ | |
Фаад |
| ||
ХЎад |
| ||
КЯМЦ |
|
ЃЈ1ЃЉШєдк![]() етШЫжаЃЌАДадБ№ЗжВуГщШЁвЛИіШнСПЮЊ
етШЫжаЃЌАДадБ№ЗжВуГщШЁвЛИіШнСПЮЊ![]() ЕФбљБОЃЌХЎадгІГщ
ЕФбљБОЃЌХЎадгІГщ![]() ШЫЃЌЧыНЋЩЯУцЕФСаСЊБэВЙГфЭъећЃЌВЂОнДЫзЪСЯФмЗёдкЗИДэЮѓЕФИХТЪВЛГЌЙ§
ШЫЃЌЧыНЋЩЯУцЕФСаСЊБэВЙГфЭъећЃЌВЂОнДЫзЪСЯФмЗёдкЗИДэЮѓЕФИХТЪВЛГЌЙ§![]() ЧАЬсЯТЃЌШЯЮЊдоГЩЁАзджњгЮЁБЪЧгыадБ№гаЙиЯЕЃП
ЧАЬсЯТЃЌШЯЮЊдоГЩЁАзджњгЮЁБЪЧгыадБ№гаЙиЯЕЃП
ЃЈ2ЃЉШєвдГщШЁбљБОЕФЦЕТЪЮЊИХТЪЃЌДгТУгЮНкДѓСПгЮПЭжаЫцЛњГщШЁ![]() ШЫдљЫЭОЋУРМЭФюЦЗЃЌМЧет
ШЫдљЫЭОЋУРМЭФюЦЗЃЌМЧет![]() ШЫжадоГЩЁАзджњгЮЁБШЫЪ§ЮЊ
ШЫжадоГЩЁАзджњгЮЁБШЫЪ§ЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФЗжВМСаКЭЪ§бЇЦкЭћ.
ЕФЗжВМСаКЭЪ§бЇЦкЭћ.
ИН: 
|
|
|
|
|
|
|
|
|
|
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊНЙЕудк![]() жсЩЯЕФЭждВ
жсЩЯЕФЭждВ![]() ЕФжааФЪЧдЕу
ЕФжааФЪЧдЕу![]() ЃЌРыаФТЪЮЊЫЋЧњЯп
ЃЌРыаФТЪЮЊЫЋЧњЯп![]() РыаФТЪЕФвЛАыЃЌжБЯп
РыаФТЪЕФвЛАыЃЌжБЯп![]() БЛЭждВ
БЛЭждВ![]() НиЕУЕФЯпЖЮГЄЮЊ
НиЕУЕФЯпЖЮГЄЮЊ![]() .жБЯп
.жБЯп![]() ЃК
ЃК ![]() гы
гы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌгыЭждВ
ЃЌгыЭждВ![]() НЛгк
НЛгк![]() СНИіЯрвьЕуЃЌЧв
СНИіЯрвьЕуЃЌЧв![]() .
.
ЃЈ1ЃЉЧѓЭждВ![]() ЕФЗНГЬЃЛ
ЕФЗНГЬЃЛ
ЃЈ2ЃЉЪЧЗёДцдкЪЕЪ§![]() ЃЌЪЙ
ЃЌЪЙ![]() ЃПШєДцдкЃЌЧѓ
ЃПШєДцдкЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ЕФШЁжЕЗЖЮЇЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉ=|xЉ2|Љ|2xЉa|ЃЌaЁЪRЃЎ
ЃЈ1ЃЉЕБa=3ЪБЃЌНтВЛЕШЪНfЃЈxЃЉЃО0ЃЛ
ЃЈ2ЃЉЕБxЁЪЃЈЉЁоЃЌ2ЃЉЪБЃЌfЃЈxЃЉЃМ0КуГЩСЂЃЌЧѓaЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉ=x2Љ2x|xЉa|ЃЈЦфжаaЁЪRЃЉЃЎ
ЃЈ1ЃЉЕБa=1ЪБЃЌЧѓКЏЪ§fЃЈxЃЉЕФжЕгђЃЛ
ЃЈ2ЃЉШєy=fЃЈxЃЉдк[0ЃЌ2]ЩЯЕФзюаЁжЕЮЊЉ1ЃЌЧѓaЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЙћвЛИіЪЕЪ§Ъ§Са{an}ТњзуЬѕМўЃК ![]() ЃЈdЮЊГЃЪ§ЃЌnЁЪN*ЃЉЃЌдђГЦетвЛЪ§СаЁАЮБЕШВюЪ§СаЁБЃЌdГЦЮЊЁАЮБЙЋВюЁБЃЎИјГіЯТСаЙигкФГИіЮБЕШВюЪ§Са{an}ЕФНсТлЃКЂйЖдгкШЮвтЕФЪзЯюa1 ЃЌ ШєdЃМ0ЃЌдђетвЛЪ§СаБиЮЊгаЧюЪ§СаЃЛЂкЕБdЃО0ЃЌa1ЃО0ЪБЃЌетвЛЪ§СаБиЮЊЕЅЕїЕндіЪ§СаЃЛЂлетвЛЪ§СаПЩвдЪЧвЛИіжмЦкЪ§СаЃЛЂмШєетвЛЪ§СаЕФЪзЯюЮЊ1ЃЌЮБЙЋВюЮЊ3ЃЌ-
ЃЈdЮЊГЃЪ§ЃЌnЁЪN*ЃЉЃЌдђГЦетвЛЪ§СаЁАЮБЕШВюЪ§СаЁБЃЌdГЦЮЊЁАЮБЙЋВюЁБЃЎИјГіЯТСаЙигкФГИіЮБЕШВюЪ§Са{an}ЕФНсТлЃКЂйЖдгкШЮвтЕФЪзЯюa1 ЃЌ ШєdЃМ0ЃЌдђетвЛЪ§СаБиЮЊгаЧюЪ§СаЃЛЂкЕБdЃО0ЃЌa1ЃО0ЪБЃЌетвЛЪ§СаБиЮЊЕЅЕїЕндіЪ§СаЃЛЂлетвЛЪ§СаПЩвдЪЧвЛИіжмЦкЪ§СаЃЛЂмШєетвЛЪ§СаЕФЪзЯюЮЊ1ЃЌЮБЙЋВюЮЊ3ЃЌ- ![]() ПЩвдЪЧетвЛЪ§СажаЕФвЛЯюЃЛnЁЪN*ЂнШєетвЛЪ§СаЕФЪзЯюЮЊ0ЃЌЕкШ§ЯюЮЊЉ1ЃЌдђетвЛЪ§СаЕФЮБЙЋВюПЩвдЪЧ
ПЩвдЪЧетвЛЪ§СажаЕФвЛЯюЃЛnЁЪN*ЂнШєетвЛЪ§СаЕФЪзЯюЮЊ0ЃЌЕкШ§ЯюЮЊЉ1ЃЌдђетвЛЪ§СаЕФЮБЙЋВюПЩвдЪЧ ![]() ЃЎЦфжае§ШЗЕФНсТлЪЧ ЃЎ
ЃЎЦфжае§ШЗЕФНсТлЪЧ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЭждВ![]() ЖЬжсЖЫЕуКЭСНИіНЙЕуЕФСЌЯпЙЙГЩе§ЗНаЮЃЌЧвИУе§ЗНаЮЕФФкЧадВЗНГЬЮЊ
ЖЬжсЖЫЕуКЭСНИіНЙЕуЕФСЌЯпЙЙГЩе§ЗНаЮЃЌЧвИУе§ЗНаЮЕФФкЧадВЗНГЬЮЊ![]() .
.
ЃЈ1ЃЉЧѓЭждВ![]() ЕФЗНГЬЃЛ
ЕФЗНГЬЃЛ
ЃЈ2ЃЉШєХзЮяЯп![]() ЕФНЙЕугыЭждВ
ЕФНЙЕугыЭждВ![]() ЕФвЛИіНЙЕу
ЕФвЛИіНЙЕу![]() жиКЯЃЌжБЯп
жиКЯЃЌжБЯп![]() гыХзЮяЯп
гыХзЮяЯп![]() НЛгкСНЕу
НЛгкСНЕу![]() ЃЌЧв
ЃЌЧв![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФУцЛ§ЕФзюДѓжЕ.
ЕФУцЛ§ЕФзюДѓжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЌ
ЃЌ ![]() .
.
ЃЈ1ЃЉЬжТлКЏЪ§![]() ЕФЕЅЕїЧјМфЃЛ
ЕФЕЅЕїЧјМфЃЛ
ЃЈ2ЃЉШє![]() ЃЌ
ЃЌ ![]() КуГЩСЂЃЌЧѓ
КуГЩСЂЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com