
【题目】选修4-4:坐标系与参数方程
在直角坐标系中,以坐标原点![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴建立极坐标系.已知点
轴的非负半轴为极轴建立极坐标系.已知点![]() 的极坐标为
的极坐标为![]() ,圆
,圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),(1)直线
为参数),(1)直线![]() 过
过![]() 且与圆
且与圆![]() 相切,求直线
相切,求直线![]() 的极坐标方程;(2)过点
的极坐标方程;(2)过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与圆
与圆![]() 交于
交于![]() ,
, ![]() 两点,若
两点,若![]() ,求实数
,求实数![]() 的值.
的值.
【答案】(1)![]() 或
或![]() .(2)-3.
.(2)-3.
【解析】试题分析:(1)先根据直线与圆相切求直线![]() 的直角坐标方程(注意斜率不存在的情形),再利用
的直角坐标方程(注意斜率不存在的情形),再利用![]() 将直角坐标方程化为极坐标方程(2)设直线
将直角坐标方程化为极坐标方程(2)设直线![]() 的参数方程,根据参数几何意义得
的参数方程,根据参数几何意义得![]() ,将直线
,将直线![]() 的参数方程代入圆
的参数方程代入圆![]() 的方程,并利用韦达定理得
的方程,并利用韦达定理得![]() ,解方程可得实数
,解方程可得实数![]() 的值.注意满足判别式大于零.
的值.注意满足判别式大于零.
试题解析:解:(1)![]() 的直角坐标为
的直角坐标为![]() ,圆
,圆![]() 的直角坐标方程为
的直角坐标方程为![]() ,
,
设直线![]() ,即
,即![]() ,
,
因为直线![]() 与圆
与圆![]() 相切,所以
相切,所以![]() ,解得
,解得![]() ,
,
此时直线![]() 的方程为
的方程为![]() ,
,
若直线![]() 的斜率不存在时,直线
的斜率不存在时,直线![]() 的方程为
的方程为![]() ,
,
所以直线![]() 的极坐标方程为
的极坐标方程为![]() 或
或![]() .
.
(2)将直线![]() 的参数方程
的参数方程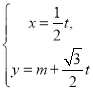 (
(![]() 时参数)代入圆
时参数)代入圆![]() 的方程
的方程![]() ,
,
得: ![]() ,
, ![]()
![]() ,
,
设![]() ,
, ![]() ,则
,则![]() ,因为
,因为![]() ,所以
,所以![]() ,
,
所以![]() ,解得
,解得![]() ,
,
由![]() 知,所求
知,所求![]() 的值为-3.
的值为-3.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知圆F1:(x+1)2+y2=16,定点F2(1,0),A是圆F1上的一动点,线段F2A的垂直平分线交半径F1A于P点.
(1)求P点的轨迹C的方程;
(2)四边形EFGH的四个顶点都在曲线C上,且对角线EG,FH过原点O,
若kEGkFH=-![]() ,求证:四边形EFGH的面积为定值,并求出此定值.
,求证:四边形EFGH的面积为定值,并求出此定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校课改实行选修走班制,现有甲,乙,丙,丁四位学生准备选修物理,化学,生物三个科目.每位学生只选修一个科目,且选修其中任何一个科目是等可能的.
(1)恰有2人选修物理的概率;
(2)选修科目个数ξ的分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近代统计学的发展起源于二十世纪初,它是在概率论的基础上发展起来的,统计性质的工作可以追溯到远古的“结绳记事”和《二十四史》中大量的关于我人口、钱粮、 水文、天文、地震等资料的记录.近几年,雾霾来袭,对某市该年11月份的天气情况进行统计,结果如下:表一
日期 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
天气 | 晴 | 霾 | 霾 | 阴 | 霾 | 霾 | 阴 | 霾 | 霾 | 霾 | 阴 | 晴 | 霾 | 霾 | 霾 |
日期 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
天气 | 霾 | 霾 | 霾 | 阴 | 晴 | 霾 | 霾 | 晴 | 霾 | 晴 | 霾 | 霾 | 霾 | 晴 | 霾 |
由于此种情况某市政府为减少雾霾于次年采取了全年限行的政策.
下表是一个调査机构对比以上两年11月份(该年不限行![]() 天、次年限行
天、次年限行![]() 天共
天共![]() 天)的调查结果:
天)的调查结果:
表二
不限行 | 限行 | 总计 | |
没有雾霾 |
| ||
有雾霾 |
| ||
总计 |
|
|
|
(1)请由表一数据求![]() ,并求在该年11月份任取一天,估计该市是晴天的概率;
,并求在该年11月份任取一天,估计该市是晴天的概率;
(2)请用统计学原理计算若没有![]() 的把握认为雾霾与限行有关系,则限行时有多少天没有雾霾?
的把握认为雾霾与限行有关系,则限行时有多少天没有雾霾?
(由于不能使用计算器,所以表中数据使用时四舍五入取整数)
|
|
|
|
|
|
|
|
|
|
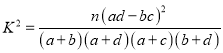
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2cosxsin(x+ ![]() )﹣a,且x=﹣
)﹣a,且x=﹣ ![]() 是方程f(x)=0的一个解.
是方程f(x)=0的一个解.
(1)求实数a的值及函数f(x)的最小正周期;
(2)求函数f(x)的单调递减区间;
(3)若关于x的方程f(x)=b在区间(0, ![]() )上恰有三个不相等的实数根x1 , x2 , x3 , 直接写出实数b的取值范围及x1+x2+x3的取值范围(不需要给出解题过程)
)上恰有三个不相等的实数根x1 , x2 , x3 , 直接写出实数b的取值范围及x1+x2+x3的取值范围(不需要给出解题过程)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(log2x﹣2)(log4x﹣ ![]() )
)
(1)当x∈[2,4]时,求该函数的值域;
(2)若f(x)>mlog2x对于x∈[4,16]恒成立,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子中有大小、质地相同的红球、黑球各一个,现有放回地随机摸取3次,每次摸取一个球,若摸出红球,得10分,摸出黑球,得5分,则3次摸球所得总分至少是25分的概率是___.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为R的函数 ![]() 是奇函数.
是奇函数.
(1)求实数a,b的值;
(2)判断f(x)在(﹣∞,+∞)上的单调性;
(3)若f(k3x)+f(3x﹣9x+2)>0对任意x≥1恒成立,求k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com