
【题目】在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求![]() 的长;
的长;
(2)若![]() ,求四边形
,求四边形![]() 的面积.
的面积.
【答案】(1)![]() (2)
(2) ![]()
【解析】
(1)由余弦定理得能求出AD的长.
(2)由正弦定理得![]() ,从而BC=3
,从而BC=3![]() ,DC
,DC![]() ,过A作AE⊥BD,交BD于E,过C作CF⊥BD,交BD于F,则可求AE
,过A作AE⊥BD,交BD于E,过C作CF⊥BD,交BD于F,则可求AE![]() ,CF
,CF![]() ,四边形ABCD的面积:S=S△ABD+S△BDC
,四边形ABCD的面积:S=S△ABD+S△BDC![]() ,由此能求出结果.
,由此能求出结果.
(1)∵在四边形ABCD中,AD∥BC,AB![]() ,∠A=120°,BD=3.
,∠A=120°,BD=3.
∴由余弦定理得:cos120°![]() ,
,
解得AD![]() (舍去AD=﹣2
(舍去AD=﹣2![]() ),
),
∴AD的长为![]() .
.
(2)∵AD∥BC,AB![]() ,∠A=120°,BD=3,AD
,∠A=120°,BD=3,AD![]() ,
,
∠BCD=105°,
∴∠DBC=30°,∠BDC=45°,
∴![]() ,
,
解得BC=3![]() ,DC
,DC![]() ,
,
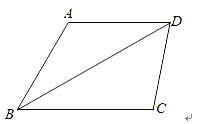
如图,过A作AE⊥BD,交BD于E,过C作CF⊥BD,交BD于F,
则AE![]() ,CF
,CF![]() ,
,
∴四边形ABCD的面积:
S=S△ABD+S△BDC![]()
![]()
![]() .
.


 优加精卷系列答案
优加精卷系列答案科目:高中数学 来源: 题型:
【题目】已知二次函数![]() .
.
(1)若![]() 的定义域和值域均是
的定义域和值域均是![]() ,求实数
,求实数![]() 的值;
的值;
(2)若![]() 在区间
在区间![]() 上是减函数,求
上是减函数,求![]() 在区间
在区间![]() 上的最小值和最大值;
上的最小值和最大值;
(3)若![]() 在区间
在区间![]() 上有零点,求实数
上有零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :在
:在![]() 轴上的一个焦点,与短轴两个端点的连线互相垂直,且右焦点坐标为
轴上的一个焦点,与短轴两个端点的连线互相垂直,且右焦点坐标为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与圆
与圆![]() 相切,和椭圆交于
相切,和椭圆交于![]() ,
,![]() 两点,
两点,![]() 为原点,线段
为原点,线段![]() ,
,![]() 分别和圆
分别和圆![]() 交于
交于![]() ,
,![]() 两点,设
两点,设![]() ,
,![]() 的面积分别为
的面积分别为![]() ,
,![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合S={1,2,3,4,5,6},一一映射f:S→S满足条件:对于任意的x∈S,有f(f(f(x)))=x。则满足条件的映射f的个数是( )。
A. 81 B. 80 C. 40 D. 27
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com