
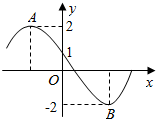
 函数f(x)=2sin(ωx+φ)的部分图象如图所示,其中A,B两点之间的距离为5,那么下列说法正确的是( )
函数f(x)=2sin(ωx+φ)的部分图象如图所示,其中A,B两点之间的距离为5,那么下列说法正确的是( )| A. | 函数f(x)的最小正周期为8 | |
| B. | f(3)=-$\frac{1}{2}$ | |
| C. | x=$\frac{3}{2}$是函数f(x)的一条对称轴 | |
| D. | 函数f(x)向右平移一个单位长度后所得的函数为偶函数 |
分析 由题意结合图象可求函数的解析式,逐个选项验证可得.
解答 解:设AB两点的水平距离为d,则d2+42=52,解得d=3,
∴函数的最小正周期为3×2=6,故A错误;
由周期为6可得ω=$\frac{π}{3}$,可得f(x)=2sin($\frac{π}{3}$x+φ),
代入点(0,1)可得1=2sinφ,可取φ=$\frac{5π}{6}$,
∴f(x)=2sin($\frac{π}{3}$x+$\frac{5π}{6}$),
∴f(3)=-1,故B错误;
令$\frac{π}{3}$x+$\frac{5π}{6}$=kπ+$\frac{π}{2}$可得x=3k-1,k∈Z,
令3k-1=$\frac{3}{2}$可得k=$\frac{15}{2}$∉Z,故C错误;
又f(x)=2sin($\frac{π}{3}$x+$\frac{5π}{6}$)向右平移一个单位长度后所得的函数
为y=2sin($\frac{π}{3}$x-$\frac{π}{3}$+$\frac{5π}{6}$)=2sin($\frac{π}{3}$x+$\frac{π}{2}$)=2cos$\frac{π}{3}$x为偶函数,故D正确.
故选:D
点评 本题考查正弦函数的图象,涉及正弦函数的对称性和图象变换,属中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示.已知直角梯形ABCD,BC∥AD,∠ABC=90°AB=5cm,BC=16cm,AD=4cm,求以AB所在直线为轴旋转一周所得几何体的表面积.
如图所示.已知直角梯形ABCD,BC∥AD,∠ABC=90°AB=5cm,BC=16cm,AD=4cm,求以AB所在直线为轴旋转一周所得几何体的表面积.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com