
【题目】已知数列![]() 满足
满足![]()
![]() ,且
,且![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设数列![]() 的前n项和为
的前n项和为![]() ,求证:当
,求证:当![]() 时,
时,![]() .
.
【答案】(1)![]() (2)证明见解析
(2)证明见解析
【解析】
(1)法一:计算出数列前4项,猜想:![]() ,用数学归纳法证明即可;法二:所给等式化简为
,用数学归纳法证明即可;法二:所给等式化简为![]() 所以
所以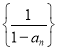 是等差数列,首项为2,公差为1,求出通项公式即可得解;(2) 先证明
是等差数列,首项为2,公差为1,求出通项公式即可得解;(2) 先证明![]() 时,
时,![]() ,
,
![]() ,再证明
,再证明![]() ,即可得证.
,即可得证.
解:(1)法一:![]() ,且
,且![]()
![]()
![]() ,
,
同样可求得![]()
![]() ,
,
猜想:![]() ,
,
以下用数学归纳法证明
①当![]() 时,
时,![]() ,符合
,符合![]() ,
,
②假设![]() 时,
时,![]()
![]() ,
,
则![]() 时,
时,![]() ,即
,即![]() ,
,
![]()
![]()
![]() 符合
符合![]() ,
,
综上:![]() .
.
法二:由![]() 得
得![]()
![]() ,
,![]() ,
,
即![]() ,
,![]()
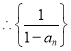 是等差数列,首项为2,公差为1,
是等差数列,首项为2,公差为1,
![]() 则
则![]() .
.
(2)当![]() 时,
时,![]()
![]() ,
,
法一:先证明![]() 时,
时,![]() ,
,
令![]()
![]() ,则
,则![]()
![]() ,
,
![]()
![]() 为减函数,
为减函数,
则![]()
![]() 时,
时,![]() .
.
![]() 时,
时,![]()
![]()
![]() ,
,
又![]()
![]() 即
即![]()
![]() ,
,
![]() 时,
时,![]() ,
,
![]() 当
当![]() 时,
时,![]() .
.
法二:![]()
![]()
![]() ,
,
![]() 要证明
要证明![]() ,
,
即证![]() ,
,
设![]() ,
,
则![]() ,
,
![]()
![]()
![]()
由![]() 得:
得:
当![]() 时,
时,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 当
当![]() 时,
时,![]() .
.
法三:由法二知即证![]()
![]() ,
,
设![]()
![]()
![]()
![]()
当![]() 时,
时,![]() 成立,
成立,
当![]() 时,
时,![]()
![]() ,
,
![]() 当
当![]() 时,
时,![]() .
.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,若同时满足以下条件:
,若同时满足以下条件:
①![]() 在D上单调递减或单调递增;
在D上单调递减或单调递增;
②存在区间![]() ,使
,使![]() 在
在![]() 上的值域是
上的值域是![]() ,那么称
,那么称![]() 为闭函数.
为闭函数.
(1)求闭函数![]() 符合条件②的区间
符合条件②的区间![]() ;
;
(2)判断函数![]() 是不是闭函数?若是请找出区间
是不是闭函数?若是请找出区间![]() ;若不是请说明理由;
;若不是请说明理由;
(3)若![]() 是闭函数,求实数
是闭函数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】王老师是高三的班主任,为了在寒假更好的督促班上的学生完成学习作业,王老师特地组建了一个QQ群,群的成员由学生、家长、老师共同组成.已知该QQ群中男学生人数多于女学生人数,女学生人数多于家长人数,家长人数多于教师人数,教师人数的两倍多于男学生人数.则该QQ群人数的最小值为( )
A.20B.22C.26D.28
查看答案和解析>>
科目:高中数学 来源: 题型:
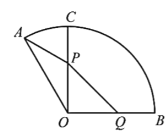
【题目】如图是一个半径为1千米的扇形景点的平面示意图,![]() .原有观光道路OC,且
.原有观光道路OC,且![]() .为便于游客观赏,景点管理部门决定新建两条道路PQ、PA,其中P在原道路OC(不含端点O、C)上,Q在景点边界OB上,且
.为便于游客观赏,景点管理部门决定新建两条道路PQ、PA,其中P在原道路OC(不含端点O、C)上,Q在景点边界OB上,且![]() ,同时维修原道路的OP段,因地形原因,新建PQ段、PA段的每千米费用分别是
,同时维修原道路的OP段,因地形原因,新建PQ段、PA段的每千米费用分别是![]() 万元、
万元、![]() 万元,维修OP段的每千米费用是
万元,维修OP段的每千米费用是![]() 万元.
万元.
(1)设![]() ,求所需总费用
,求所需总费用![]() ,并给出
,并给出![]() 的取值范围;
的取值范围;
(2)当P距离O处多远时,总费用最小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() ,
,![]() 为其前
为其前![]() 项的和,满足
项的和,满足![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设数列![]() 的前
的前![]() 项和为
项和为![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,求证:当
,求证:当![]() ,
,![]() 时
时![]() ;
;
(3)已知当![]() ,且
,且![]() 时有
时有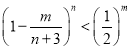 ,其中
,其中![]() ,求满足
,求满足![]() 的所有
的所有![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点
的两个焦点![]() ,
,![]() 与短轴的一个端点构成一个等边三角形,且直线
与短轴的一个端点构成一个等边三角形,且直线![]() 与圆
与圆![]() 相切.
相切.
(1)求椭圆![]() 的方程;
的方程;
(2)已知过椭圆![]() 的左顶点
的左顶点![]() 的两条直线
的两条直线![]() ,
,![]() 分别交椭圆
分别交椭圆![]() 于
于![]() ,
,![]() 两点,且
两点,且![]() ,求证:直线
,求证:直线![]() 过定点,并求出定点坐标;
过定点,并求出定点坐标;
(3)在(2)的条件下求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某健身馆在2019年7、8两月推出优惠项目吸引了一批客户.为预估2020年7、8两月客户投入的健身消费金额,健身馆随机抽样统计了2019年7、8两月100名客户的消费金额,分组如下:![]() ,
,![]() ,
,![]() ,…,
,…,![]() (单位:元),得到如图所示的频率分布直方图:
(单位:元),得到如图所示的频率分布直方图:
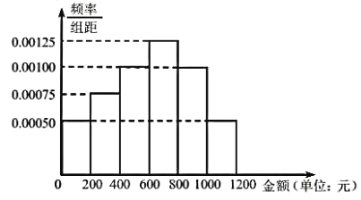
(1)请用抽样的数据预估2020年7、8两月健身客户人均消费的金额(同一组中的数据用该组区间的中点值作代表);
(2)若把2019年7、8两月健身消费金额不低于800元的客户,称为“健身达人”,经数据处理,现在列联表中得到一定的相关数据,请补全空格处的数据,并根据列联表判断是否有![]() 的把握认为“健身达人”与性别有关?
的把握认为“健身达人”与性别有关?
健身达人 | 非健身达人 | 总计 | |
男 | 10 | ||
女 | 30 | ||
总计 |
(3)为吸引顾客,在健身项目之外,该健身馆特别推出健身配套营养品的销售,现有两种促销方案.
方案一:每满800元可立减100元;
方案二:金额超过800元可抽奖三次,每次中奖的概率为![]() ,且每次抽奖互不影响,中奖1次打9折,中奖2次打8折,中奖3次打7折.
,且每次抽奖互不影响,中奖1次打9折,中奖2次打8折,中奖3次打7折.
若某人打算购买1000元的营养品,请从实际付款金额的数学期望的角度分析应该选择哪种优惠方案.
附:
| 0.100 | 0.050 | 0.010 | 0.005 | |
| 2.072 | 2.706 | 3.841 | 6.635 | 7.879 |
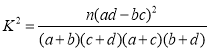
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】提高过江大桥的车辆通行能力可改善整个城市的交通状况,在一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当20≤x≤200时,车流速度v是车流密度x的一次函数.
(1)当0≤x≤200时,求函数v(x)的表达式;
(2)当车流密度x为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)f(x)=xv(x)可以达到最大,并求出最大值.(精确到1辆/小时).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com