练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    ．（本小题满分14分）甲乙两人连续年对某县农村鳗鱼养殖业的规模(总产量)进行调查,提供了两个方面的信息,分别得到甲、乙两图：

    甲调查表明：每个鱼池平均产量从第年万只鳗鱼上升到第年万只。
    乙调查表明：全县鱼池总个数由第年个减少到第年个。
    （1）求第年全县鱼池的个数及全县出产的鳗鱼总数；
    （2）哪一年的规模(即总产量)最大?请说明理由.
    解：由题意可知,图甲图象经过和两点,
    从而求得其解析式为       ………2分
    图乙图象经过和两点,
    从而求得其解析式为          ………………4分
    （1）当时，,  ……6分
    ∴
    ∴第年鱼池有个,全县出产的鳗鱼总数为万只.   ………………7分
    (2)设第年时的规模总产量为,
    则 …10分
    对称轴  ，开口向下，又   
    ∴ 当时，有最大值……13分
    答：第年时鳗鱼养殖业的规模最大,最大产量为万只.    ………14分
    略
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：单选题

    若函数等于
    A．0B．1C．2D．4

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    设，，，实数a满足＞0，那么当x＞1时必有（   ）
    A．＜＜B．＜＜
    C．＜＜D．＜＜

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    下列函数中，满足“对任意，，当时，”的是
    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    、出租车几何学是由十九世纪的赫尔曼-闵可夫斯基所创立的。在出租车几何学中，点还是形如的有序实数对，直线还是满足的所有组成的图形，角度大小的定义也和原来一样。直角坐标系内任意两点定义它们之间的一种“距离”：，请解决以下问题：
    1、（理）求线段上一点的距离到原点的“距离”；
    （文）求点、的“距离”；
    2、（理）定义:“圆”是所有到定点“距离”为定值的点组成的图形，
    求“圆周”上的所有点到点 的“距离”均为 的“圆”方程；
    （文）求线段上一点的距离到原点的“距离”；
    3、（理）点、，写出线段的垂直平分线的轨迹方程并画出大致图像．
    （文）定义:“圆”是所有到定点“距离”为定值的点组成的图形，点、，，求经过这三个点确定的一个“圆”的方程，并画出大致图像；
    （说明所给图形小正方形的单位是1）

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （本小题满分12分）
    已知函数
    1）讨论并证明函数)在区间的单调性；
    2）若对任意的恒成立，求实数的取值范围。

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    对于函数定义域中任意的x1，x2（x1≠x2）有如下结论：
    ①         ②
    ③                 ④
    当时，上述结论中正确的是（   ）
    A．②③B．②④C．①③D．①④

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （本题满分14分）
    定义在R上的单调函数满足，且对任意都有

    （I）试求的值并证明函数为奇函数；
    （II）若对任意恒成立，求实数m的取值范围。

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

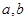    已知两个正数,可按规则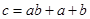扩充为一个新数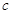,在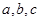三个数中取两个较大的数,按上述规则扩充得到一个新数，依次下去，将每扩充一次得到一个新数称为一次操作.
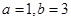    （1）若,按上述规则操作三次,扩充所得的数是__________；
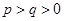    （2）若，经过6次操作后扩充所得的数为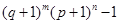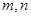（为正整数），则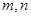的值分别为____________

    查看答案和解析>>

    同步练习册答案