
【题目】如图,ABCD为直角梯形,∠C=∠CDA=90°,AD=2BC=2CD=2,P为平面ABCD外一点,且PB⊥BD.
(1)求证:PA⊥BD;
(2)若直线l过点P,且直线l∥直线BC,试在直线l上找一点E,使得直线PC∥平面EBD;
(3)若PC⊥CD,PB=4,求四棱锥P﹣ABCD的体积.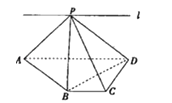
【答案】证明:(1)∵ABCD为直角梯形,AD=![]() AB=
AB=![]() BD,
BD,
∴AB⊥BD,
∵PB⊥BD,AB∩PB=B,AB,PB平面PAB,
BD⊥平面PAB,
∵PA面PAB,∴PA⊥BD;
(2)解:在上l取一点E,使PE=BC,
∵PE∥BC,∴四边形BCPE是平行四边形,
∴PC∥BE,PC平面EBD,BE平面EBD
∴PC∥平面EBD;
(3)解:∵PC⊥CD,DC⊥BC,PC∩BC=C,
∴DC⊥平面PBC,
∴DC⊥PB,
∵PB⊥BD,BD∩DC=D,
∴PB⊥平面ABCD,
∴四棱锥P﹣ABCD的体积为![]() =2.
=2.
【解析】(1)要证PA⊥BD,只需证明AB⊥BD、PB⊥BD(因为PA、PB是平面PAB内的两条相交直线);
(2)在上l取一点E,使PE=BC,利用直线l∥直线BC,推出PC∥BE,可以证明直线PC∥平面EBD;
(3)证明PB⊥平面ABCD,再求四棱锥P﹣ABCD的体积.
【考点精析】本题主要考查了空间中直线与直线之间的位置关系和直线与平面平行的判定的相关知识点,需要掌握相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点;平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行才能正确解答此题.


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】共享单车已成为一种时髦的新型环保交通工具,某共享单车公司为了拓展市场,对![]() ,
,![]() 两个品牌的共享单车在编号分别为1,2,3,4,5的五个城市的用户人数(单位:十万)进行统计,得到数据如下:
两个品牌的共享单车在编号分别为1,2,3,4,5的五个城市的用户人数(单位:十万)进行统计,得到数据如下:
城市品牌 | 1 | 2 | 3 | 4 | 5 |
| 3 | 4 | 12 | 6 | 8 |
| 4 | 3 | 7 | 9 | 5 |
(Ⅰ)若共享单车用户人数超过50万的城市称为“优城”,否则称为“非优城”,据此判断能否有![]() 的把握认为“优城”和共享单车品牌有关?
的把握认为“优城”和共享单车品牌有关?
(Ⅱ)若不考虑其它因素,为了拓展市场,对![]() 品牌要从这五个城市选择三个城市进行宣传.
品牌要从这五个城市选择三个城市进行宣传.
(i)求城市2被选中的概率;
(ii)求在城市2被选中的条件下城市3也被选中的概率.
附:参考公式及数据
| 0.15 | 0.10 | 0.05 | 0.025 | 0.005 | 0.001 | |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的离心率e=
的离心率e=![]() , 原点到过A(a,0),B(0,﹣b)两点的直线的距离是
, 原点到过A(a,0),B(0,﹣b)两点的直线的距离是![]() .
.
(1)求椭圆的方程;
(2)已知直线y=kx+1(k≠0)交椭圆于不同的两点E,F,且E,F都在以B为圆心的圆上,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电信公司从所在地的1000名使用4G手机用户中,随机抽取了20名,对其收集每日使用流量(单位:M)进行统计,得到如下数据:
流量x | 0≤x<5 | 5≤x<10 | 10≤x<15 | 15≤x<20 | 20≤x<25 | x≥25 |
人数 | 1 | 6 | 6 | 5 | 2 | 0 |
(1)估计这20名4G手机用户每日使用流量(单位:M)的平均值;
(2)估计此地1000名使用4G手机用户中每日使用流量不少于10M用户数;
(3)在15≤x<20和20≤x<25两组用户中,随机抽取两人作进一步问卷调查,求所抽取的两人恰好来自不同组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)设直线![]() 的方程为
的方程为![]() .若直线
.若直线![]() 在两坐标轴上的截距相等,求直线
在两坐标轴上的截距相等,求直线![]() 的方程;
的方程;
(2)过直线![]() :
:![]() 上的点
上的点![]() 作直线
作直线![]() ,若直线
,若直线![]() ,
,![]() 与
与![]() 轴围成的三角形的面积为2,则直线
轴围成的三角形的面积为2,则直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com