解:(1)f′(x)=8x
2-4x+b,△=16-32b
①当△≤0即b≥

时,f′(x)≥0在R上恒成立,∴f(x)在(-∞,+∞)上单调递增;
②当△>0即b<

时,由f′(x)=0得x
1=
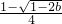
,x
2=
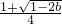
若f′(x)>0,则x<
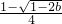
或x>
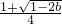
若f′(x)>0,则
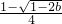
<x<
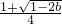
∴f(x)的单调增区间为:(-∞,
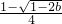
],[
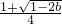
,+∞);f(x) 的单调减区间为:[
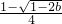
,
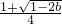
]
综上所述:当b≥

时,f(x)在(-∞,+∞)上单调递增;当b<

时,f(x)的单调增区间为:(-∞,
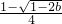
],[
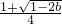
,+∞);f(x) 的单调减区间为:[
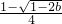
,
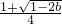
]
…(4分)
(2)g′(x)=

+1=
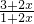
,令g′(x)=3得:x=0,∴切点为(0,0),∴f(0)=0,∴a=0
∵f′(x)=8x
2-4x+b|
x=0=b=3,∴a=0,b=3 …(6分)
令φ(x)=f(x)-g(x),则φ′(x)=f′(x)-g′(x)=
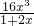
∴φ(x)在(-

,0)上单调递减,在(0,+∞)单调递增,
∴φ(x)≥φ(0)=f(0)-g(0)=0
∴φ(x)≥0 即:f(x)≥g(x) …(8分)
(3)K
AC=
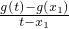
,K
BC=
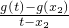
令h(t)=(1+2t)(g(t)-g(x
1))-(3+2t)(t-x
1)
则h′(t)=2 (g(t)-g(x
1))+(1+2t)g′(t)-2(t-x
1)-(3+2t)=2 (g(t)-g(x
1))-2(t-x
1)=2(ln(1+2t)-ln(1+2x
1))
∵y=ln(1+2x)在(-

,+∞)上单调递增,且t>x
1,
∴ln(1+2t)-ln(1+2x
1)>0,∴h′(t)>0
∴h(t)在(x
1,t)上单调递增,∴h(t)>h(x
1)=0
∴(1+2t)(f(t)-f(x
1))-(3+2t)(t-x
1)>0
∴(1+2t)(f(t)-f(x
1))>(3+2t)(t-x
1)
∵t-x
1>0,1+2t>0,∴
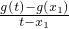
>

即K
AC>

同理可证:K
BC<

∴K
AC>K
BC即割线AC的斜率大于割线BC的斜率;…(12分)
分析:(1)求导函数,计算判别式,利用导数的正负,即可确定函数的单调区间;
(2)求出g′(x),令g′(x)=3可得切点的坐标,可求a的值,利用f′(x)=3,可求b的值.构造函数φ(x)=f(x)-g(x),求导函数,确定函数的单调性,证明φ(x)≥0即可;
(3)K
AC=
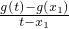
,K
BC=
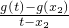
,构造h(t)=(1+2t)(g(t)-g(x
1))-(3+2t)(t-x
1),证明h(t)>0,可得K
AC>

,同理可证:K
BC<

,从而可得结论.
点评:本题考查导数知识的运用,考查函数的单调性,考查不等式的证明,解题的关键是构造函数,利用导数求解.

 x3-2x2+bx+a,g(x)=ln(1+2x)+x.
x3-2x2+bx+a,g(x)=ln(1+2x)+x. <x1<t<x2,求证:割线AC的斜率大于割线BC的斜率.
<x1<t<x2,求证:割线AC的斜率大于割线BC的斜率. 时,f′(x)≥0在R上恒成立,∴f(x)在(-∞,+∞)上单调递增;
时,f′(x)≥0在R上恒成立,∴f(x)在(-∞,+∞)上单调递增; 时,由f′(x)=0得x1=
时,由f′(x)=0得x1=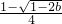 ,x2=
,x2=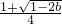
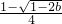 或x>
或x>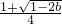
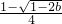 <x<
<x<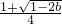
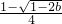 ],[
],[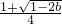 ,+∞);f(x) 的单调减区间为:[
,+∞);f(x) 的单调减区间为:[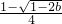 ,
,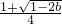 ]
] 时,f(x)在(-∞,+∞)上单调递增;当b<
时,f(x)在(-∞,+∞)上单调递增;当b< 时,f(x)的单调增区间为:(-∞,
时,f(x)的单调增区间为:(-∞,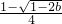 ],[
],[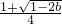 ,+∞);f(x) 的单调减区间为:[
,+∞);f(x) 的单调减区间为:[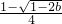 ,
,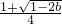 ]
] +1=
+1=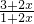 ,令g′(x)=3得:x=0,∴切点为(0,0),∴f(0)=0,∴a=0
,令g′(x)=3得:x=0,∴切点为(0,0),∴f(0)=0,∴a=0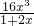
 ,0)上单调递减,在(0,+∞)单调递增,
,0)上单调递减,在(0,+∞)单调递增,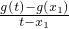 ,KBC=
,KBC=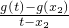
 ,+∞)上单调递增,且t>x1,
,+∞)上单调递增,且t>x1,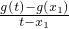 >
> 即KAC>
即KAC>

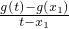 ,KBC=
,KBC=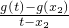 ,构造h(t)=(1+2t)(g(t)-g(x1))-(3+2t)(t-x1),证明h(t)>0,可得KAC>
,构造h(t)=(1+2t)(g(t)-g(x1))-(3+2t)(t-x1),证明h(t)>0,可得KAC> ,同理可证:KBC<
,同理可证:KBC< ,从而可得结论.
,从而可得结论.

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<