Question

如图，ABCD是边长为3的正方形，DE⊥平面ABCD，AF∥DE，DE＝3AF，BE与平面ABCD所成的角为60°.

(1)求证：AC⊥平面BDE；

(2)求二面角F-BE-D的余弦值；

(3)设点M是线段BD上一个动点，试确定点M的位置，使得AM∥平面BEF，并证明你的结论．

 

Answer 1

(1)见解析(2) (3) 点M是线段BD上靠近B点的三等分点

【解析】(1)证明　∵DE⊥平面ABCD，∴DE⊥AC，∵四边形ABCD是正方形，

∴AC⊥BD，又DE∩BD＝D，

∴AC⊥平面BDE.

(2)解　DE⊥平面ABCD，

∴∠EBD就是BE与平面ABCD所成的角，即∠EBD＝60°.

∴＝.由AD＝3，得BD＝3，DE＝3，AF＝.

如图，分别以DA，DC，DE所在直线为x轴，y轴，z轴建立空间直角坐标系，则A(3,0,0)，F(3,0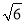，)，E(0,0，3)，B(3,3,0)，C(0，3,0)．

∴＝(0，－3，)，＝(3,0，－2)．

设平面BEF的法向量为n＝(x，y，z)，则即

令z＝，则n＝(4,2，)

∵AC⊥平面BDE，

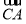∴＝(3，－3,0)为平面BDE的一个法向量，

∵cos〈n，〉＝＝＝，

∴结合图形知二面角F-BE-D的余弦值为.

(3)解　依题意，设M(t，t,0)(0≤t＜3)，则＝(t－3，t,0)，

∵AM∥平面BEF，∴·n＝0，

即4(t－3)＋2t＝0，解得t＝2.

∴点M的坐标为(2,2,0)，此时＝，

∴点M是线段BD上靠近B点的三等分点．