
【题目】如图,在正三棱柱ABC-A1B1C1中,AB=AA1=2,点P,Q分别为A1B1,BC的中点.
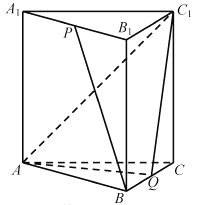
(1)求异面直线BP与AC1所成角的余弦值;
(2)求直线CC1与平面AQC1所成角的正弦值.
【答案】(1)![]()
(2)![]()
【解析】分析:(1)先建立空间直角坐标系,设立各点坐标,根据向量数量积求得向量![]() 的夹角,再根据向量夹角与异面直线所成角的关系得结果;(2)利用平面的方向量的求法列方程组解得平面
的夹角,再根据向量夹角与异面直线所成角的关系得结果;(2)利用平面的方向量的求法列方程组解得平面![]() 的一个法向量,再根据向量数量积得向量夹角,最后根据线面角与所求向量夹角之间的关系得结果.
的一个法向量,再根据向量数量积得向量夹角,最后根据线面角与所求向量夹角之间的关系得结果.
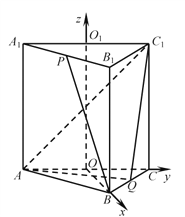
详解:如图,在正三棱柱ABCA1B1C1中,设AC,A1C1的中点分别为O,O1,则OB⊥OC,OO1⊥OC,OO1⊥OB,以![]() 为基底,建立空间直角坐标系Oxyz.
为基底,建立空间直角坐标系Oxyz.
因为AB=AA1=2,
所以![]() .
.
(1)因为P为A1B1的中点,所以![]() ,
,
从而![]() ,
,
故 .
.
因此,异面直线BP与AC1所成角的余弦值为![]() .
.
(2)因为Q为BC的中点,所以![]() ,
,
因此![]() ,
,![]() .
.
设n=(x,y,z)为平面AQC1的一个法向量,
则 即
即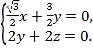
不妨取![]() ,
,
设直线CC1与平面AQC1所成角为![]() ,
,
则 ,
,
所以直线CC1与平面AQC1所成角的正弦值为![]() .
.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:高中数学 来源: 题型:
【题目】在新中国成立70周年国庆阅兵庆典中,众多群众在脸上贴着一颗红心,以此表达对祖国的热爱之情,在数学中,有多种方程都可以表示心型曲线,其中有著名的笛卡尔心型曲线,如图,在直角坐标系中,以原点O为极点,x轴正半轴为极轴建立极坐标系.图中的曲线就是笛卡尔心型曲线,其极坐标方程为![]() (
(![]() ),M为该曲线上的任意一点.
),M为该曲线上的任意一点.
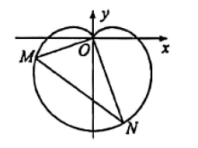
(1)当![]() 时,求M点的极坐标;
时,求M点的极坐标;
(2)将射线OM绕原点O逆时针旋转![]() 与该曲线相交于点N,求
与该曲线相交于点N,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校健康社团为调查本校大学生每周运动的时长,随机选取了80名学生,调查他们每周运动的总时长(单位:小时),按照![]()
![]()
![]()
![]()
![]()
![]() 共6组进行统计,得到男生、女生每周运动的时长的统计如下(表1、2),规定每周运动15小时以上(含15小时)的称为“运动合格者”,其中每周运动25小时以上(含25小时)的称为“运动达人”.
共6组进行统计,得到男生、女生每周运动的时长的统计如下(表1、2),规定每周运动15小时以上(含15小时)的称为“运动合格者”,其中每周运动25小时以上(含25小时)的称为“运动达人”.
表1:男生
时长 |
|
|
|
|
|
|
人数 | 2 | 8 | 16 | 8 | 4 | 2 |
表2:女生
时长 |
|
|
|
|
|
|
人数 | 0 | 4 | 12 | 12 | 8 | 4 |
(1)从每周运动时长不小于20小时的男生中随机选取2人,求选到“运动达人”的概率;
(2)根据题目条件,完成下面![]() 列联表,并判断能否有99%的把握认为本校大学生是否为“运动合格者”与性别有关.
列联表,并判断能否有99%的把握认为本校大学生是否为“运动合格者”与性别有关.
每周运动的时长小于15小时 | 每周运动的时长不小于15小时 | 总计 | |
男生 | |||
女生 | |||
总计 | |||
参考公式: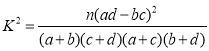 ,其中
,其中![]() .
.
参考数据:
| 0.40 | 0.25 | 0.10 | 0.010 |
| 0.708 | 1.323 | 2.706 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() ,
,![]() 分别为棱
分别为棱![]() ,
,![]() ,
,![]() ,
,![]() 的中点.
的中点.
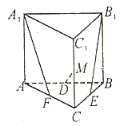
(I)证明:直线![]() 与
与![]() 共面;
共面;
(Ⅱ)证明:平面![]() 平面
平面![]() ;并试写出
;并试写出![]() 到平面
到平面![]() 的距离(不必写出计算过程).
的距离(不必写出计算过程).
查看答案和解析>>
科目:高中数学 来源: 题型:
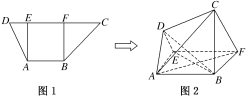
【题目】如图1,在高为2的梯形ABCD中,AB∥CD,AB=2,CD=5,过A,B分别作AE⊥CD,BF⊥CD,垂足分别为E,F.已知DE=1,将梯形ABCD沿AE,BF同侧折起,得空间几何体ADEBCF,如图2.若DE∥CF,CD=![]() ,在线段AB上是否存在点P,使得CP与平面ACD所成角的正弦值为
,在线段AB上是否存在点P,使得CP与平面ACD所成角的正弦值为![]() ?并说明理由.
?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义域是![]() 上的连续函数
上的连续函数![]() 图像的两个端点为
图像的两个端点为![]() 、
、![]() ,
,![]() 是图像
是图像![]() 上任意一点,过点
上任意一点,过点![]() 作垂直于
作垂直于![]() 轴的直线
轴的直线![]() 交线段
交线段![]() 于点
于点![]() (点
(点![]() 与点
与点![]() 可以重合),我们称
可以重合),我们称![]() 的最大值为该函数的“曲径”,下列定义域是
的最大值为该函数的“曲径”,下列定义域是![]() 上的函数中,曲径最小的是( )
上的函数中,曲径最小的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l与抛物线C:y2=4x交于A,B两点,M(2,y0)(y0≠0)为弦AB的中点,过M作AB的垂线交x轴于点P
(1)求点P的坐标;
(2)当弦AB最长时,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“一带一路”是“丝绸之路经济带”和“21世纪海上丝绸之路”的简称,旨在积极发展我国与沿线国家经济合作关系,共同打造政治互信、经济融合、文化包容的命运共同体.自2013年以来,“一带一路”建设成果显著.下图是2013-2017年,我国对“一带一路”沿线国家进出口情况统计图.下列描述错误的是( )
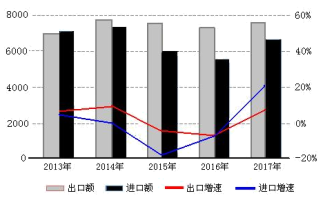
A.这五年,2013年出口额最少
B.这五年,出口总额比进口总额多
C.这五年,出口增速前四年逐年下降
D.这五年,2017年进口增速最快
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,随着![]() 网络的普及和智能手机的更新换代,各种方便的
网络的普及和智能手机的更新换代,各种方便的![]() 相继出世,其功能也是五花八门.某大学为了调查在校大学生使用
相继出世,其功能也是五花八门.某大学为了调查在校大学生使用![]() 的主要用途,随机抽取了
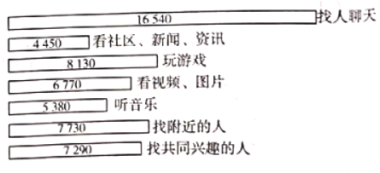
的主要用途,随机抽取了![]() 名大学生进行调查,各主要用途与对应人数的结果统计如图所示,现有如下说法:
名大学生进行调查,各主要用途与对应人数的结果统计如图所示,现有如下说法:
①可以估计使用![]() 主要听音乐的大学生人数多于主要看社区、新闻、资讯的大学生人数;
主要听音乐的大学生人数多于主要看社区、新闻、资讯的大学生人数;
②可以估计不足![]() 的大学生使用
的大学生使用![]() 主要玩游戏;
主要玩游戏;
③可以估计使用![]() 主要找人聊天的大学生超过总数的
主要找人聊天的大学生超过总数的![]() .
.
其中正确的个数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com