
| AC |
| AB |
| OA |
| OB |
| OB |
| OC |
| OC |
| OA |
| OP |
| OA |
| AB |
| AC |
| OA |
| OB |
| OC |
| 0 |
| S△AOC |
| S△ABC |
| 1 |
| 3 |
| ||
|
|
| ||
|
|
| BC |
| ||
|
|
| ||
|
|
| 1 |
| 2 |
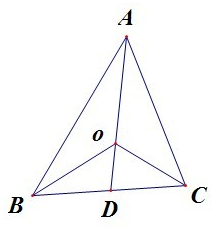
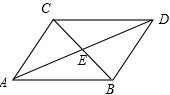 解:①若
解:①若| AC |
| AB |
| OA |
| OB |
| OB |
| OC |
| OA |
| OC |
| OB |
| AC |
| OB |
| AC |
| OB |
| AB |
| OC |
| OP |
| OA |
| AB |
| AC |
| OP |
| OA |
| AB |
| AC |
| OA |
| OB |
| OC |
| 0 |
| OC |
| OB |
| OA |
| AO |
| AO |
| OE |
| S△AOC |
| S△ADC |
| 2 |
| 3 |
| S△ADC |
| S△ABC |
| 1 |
| 2 |
| S△AOC |
| S△ABC |
| S△AOC |
| S△ADC |
| S△ADC |
| S△ABC |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| ||
|
|
| ||
|
|
| BC |
| ||
|
|
| ||
|
|
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 3 |


科目:高中数学 来源: 题型:
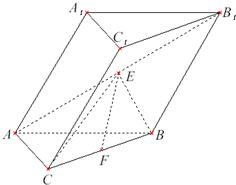 如图,在斜三棱柱ABC-A1B1C1中,AC=BC,AC⊥BC.侧面A1ABB1是边长为a的菱形,且垂直于底面ABC,∠A1AB=60°,E,F分别是AB1,BC的中点.
如图,在斜三棱柱ABC-A1B1C1中,AC=BC,AC⊥BC.侧面A1ABB1是边长为a的菱形,且垂直于底面ABC,∠A1AB=60°,E,F分别是AB1,BC的中点. | 3 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
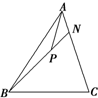 给出下列三个命题:
给出下列三个命题:| 1 |
| 2 |
| 1-cos x |
| 1+cos x |
| x |
| 2 |
| 1 |
| 2 |
| AN |
| 1 |
| 3 |
| NC |
| AP |
| AB |
| 2 |
| 11 |
| AC |
| 3 |
| 11 |
查看答案和解析>>
科目:高中数学 来源:福建省厦门六中2011-2012学年高一下学期期中考试数学试题 题型:022
如图,将边长为1的正方形ABCD沿对角线AC折起,使得平面ADC⊥平面ABC,在折起后形成的三棱锥D-ABC中,给出下列三个命题:
①△DBC是等边三角形;
②AC⊥BD;
③三棱锥D-ABC的体积是![]() .
.

其中正确命题的序号是________.(写出所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点)和点A1.
(1)画出一个格点△A1B1C1,![]() 并使它与△ABC全等且A与A1是对应点;
并使它与△ABC全等且A与A1是对应点;

(2)画出点B关于直线AC的对称点D,并指出AD可以看作由AB绕A点经过怎样的旋转而得到的.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年北京市西城区普通校高二(上)期中数学试卷(解析版) 题型:解答题
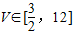 ,求a的取值范围.
,求a的取值范围.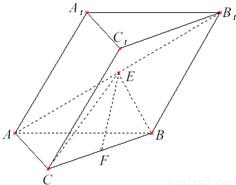
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com