
【题目】如图,![]() ,
,![]() ,…,
,…,![]() 是曲线
是曲线![]() :
:![]() 上的点,
上的点,![]() ,
,![]() ,…,
,…,![]() 是
是![]() 轴正半轴上的点,且
轴正半轴上的点,且![]() ,
,![]() ,…,
,…,![]() 均为斜边在
均为斜边在![]() 轴上的等腰直角三角形(
轴上的等腰直角三角形(![]() 为坐标原点).
为坐标原点).
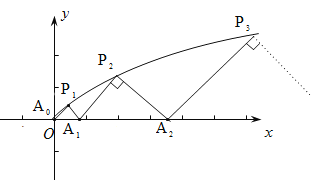
(1)写出![]() 、
、![]() 和
和![]() 之间的等量关系,以及
之间的等量关系,以及![]() 、
、![]() 和
和![]() 之间的等量关系;
之间的等量关系;
(2)猜测并证明数列![]() 的通项公式;
的通项公式;
(3)设![]() ,集合
,集合![]() ,
,![]() ,若
,若![]() ,求实常数
,求实常数![]() 的取值范围.
的取值范围.
 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:
【题目】已知数列![]() 、
、![]() ,其中,
,其中,![]() ,数列{bn}满足b1=2,bn+1=2bn.
,数列{bn}满足b1=2,bn+1=2bn.
(1)求数列![]() 、
、![]() 的通项公式;
的通项公式;
(2)是否存在自然数![]() ,使得对于任意
,使得对于任意![]() ,
,![]() ,有
,有![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的最小值;
的最小值;
(3)若数列![]() 满足
满足![]()
 ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小学为了解四年级学生的家庭作业用时情况,从本校四年级随机抽取了一批学生进行调查,并绘制了学生作业用时的频率分布直方图,如图所示.
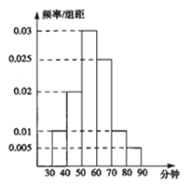
(1)估算这批学生的作业平均用时情况;
(2)作业用时不能完全反映学生学业负担情况,这与学生自身的学习习惯有很大关系如果用时四十分钟之内评价为优异,一个小时以上为一般,其它评价为良好.现从优异和良好的学生里面用分层抽样的方法抽取300人,其中女生有90人(优异20人).请完成列联表,并根据列联表分析能否在犯错误的概率不超过0.05的前提下认为学习习惯与性别有关系?
男生 | 女生 | 合计 | |
良好 | |||
优异 | |||
合计 |
附:![]() ,其中
,其中![]()
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着计算机的出现,图标被赋予了新的含义,又有了新的用武之地.在计算机应用领域,图标成了具有明确指代含义的计算机图形.如图所示的图标是一种被称之为“黑白太阳”的图标,该图标共分为3部分.第一部分为外部的八个全等的矩形,每一个矩形的长为3、宽为1;第二部分为圆环部分,大圆半径为3,小圆半径为2;第三部分为圆环内部的白色区域.在整个“黑白太阳”图标中随机取一点,则此点取自图标第三部分的概率为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】微信是腾讯公司推出的一种手机通讯软件,它支持发送语音短信、视频、图片和文字,一经推出便风靡全国,甚至涌现出一批在微信的朋友圈内销售商品的人(被称为微商).为了调查每天微信用户使用微信的时间,某经销化妆品的微商在一广场随机采访男性、女性用户各![]() 名,将男性、女性使用微信的时间分成
名,将男性、女性使用微信的时间分成![]() 组:
组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别加以统计,得到如图所示的频率分布直方图.
分别加以统计,得到如图所示的频率分布直方图.

(1)根据女性频率分布直方图,估计女性使用微信的平均时间;
(2)若每天玩微信超过![]() 小时的用户列为“微信控”,否则称其为“非微信控”,请你根据已知条件完成
小时的用户列为“微信控”,否则称其为“非微信控”,请你根据已知条件完成![]() 的列联表,并判断是否有
的列联表,并判断是否有![]() 的把握认为“微信控”与“性别”有关?
的把握认为“微信控”与“性别”有关?
参考公式:![]() ,其中
,其中![]() .
.
参考数据:

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点与短轴的一个端点是等边三角形的三个顶点,且长轴长为4
的两个焦点与短轴的一个端点是等边三角形的三个顶点,且长轴长为4
(1)求椭圆![]() 的方程;
的方程;
(2)若![]() 是椭圆
是椭圆![]() 的左顶点,经过左焦点
的左顶点,经过左焦点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点,求
两点,求![]() 与
与![]() 的面积之差的绝对值的最大值,并求取得最大值时直线
的面积之差的绝对值的最大值,并求取得最大值时直线![]() 的方程.
的方程.![]() 为坐标原点)
为坐标原点)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com