

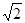 +1)ab+
+1)ab+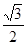 a2;(2)
a2;(2)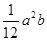 .
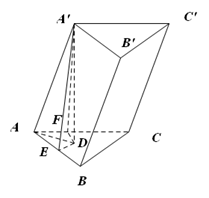
.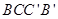 的面积,要分析它的特征,如图,过A'作A'D⊥平面ABC于点D,过点D作DE⊥AB于点E,DF⊥AC于点F,连接A'E,A'F,AD.由题意可知∠A'AE=∠A'AF=45°,AA'=AA',于是Rt△A'AE≌Rt△A'AF.,因此A'E=A'F,从而可得DE=DF.故AD平分∠BAC,又∵AB=AC,∴BC⊥AD.故BC⊥AA'.∵AA'∥BB',∴BC⊥BB'.因此四边形BCC'B'是矩形,故斜三棱柱的侧面积为2×a×bsin45°+ab=(
的面积,要分析它的特征,如图,过A'作A'D⊥平面ABC于点D,过点D作DE⊥AB于点E,DF⊥AC于点F,连接A'E,A'F,AD.由题意可知∠A'AE=∠A'AF=45°,AA'=AA',于是Rt△A'AE≌Rt△A'AF.,因此A'E=A'F,从而可得DE=DF.故AD平分∠BAC,又∵AB=AC,∴BC⊥AD.故BC⊥AA'.∵AA'∥BB',∴BC⊥BB'.因此四边形BCC'B'是矩形,故斜三棱柱的侧面积为2×a×bsin45°+ab=(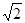 +1)ab.又∵斜三棱柱的底面积为2×
+1)ab.又∵斜三棱柱的底面积为2×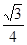 a2=
a2=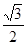 a2,∴斜三棱柱的表面积为(
a2,∴斜三棱柱的表面积为(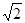 +1)ab+
+1)ab+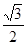 a2.(2)求B'-ABC的体积,要求出底面ABC的面积
a2.(2)求B'-ABC的体积,要求出底面ABC的面积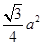 ,高
,高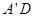 的求解根据
的求解根据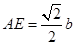 ,
,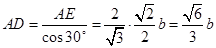 ,
,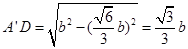 ,
,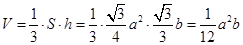 .
.
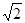 +1)ab.
+1)ab.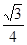 a2=
a2=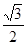 a2,∴斜三棱柱的表面积为(
a2,∴斜三棱柱的表面积为(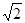 +1)ab+
+1)ab+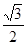 a2.
a2.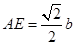 ,
,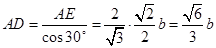 ,
,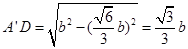 ,所以
,所以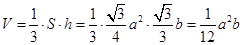 .
.

科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com