
【题目】某厂生产某种零件,每个零件的成本为40元,出厂单价定为60元,该厂为鼓励销售商订购,决定当一次订购量超过100个时,每多订购一个,订购的全部零件的出厂单价就降低0.02元,但实际出厂单价不能低于51元.
(1)当一次订购量为多少个时,零件的实际出厂单价恰降为51元?
(2)设一次订购量为x个,零件的实际出厂单价为P元,写出函数P=f(x)的表达式;
(3)当销售商一次订购500个零件时,该厂获得的利润是多少元?如果订购1000个,利润又是多少元?(工厂售出一个零件的利润=实际出厂单价﹣成本)
【答案】
(1)解:设每个零件的实际出厂价恰好降为51元时,一次订购量为x0个,则 ![]()
因此,当一次订购量为550个时,每个零件的实际出厂价恰好降为51元
(2)解:当0<x≤100时,P=60
当100<x<550时, ![]()
当x≥550时,P=51
所以 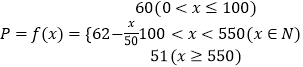
(3)解:设销售商的一次订购量为x个时,工厂获得的利润为L元,
则 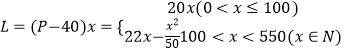
当x=500时,L=6000;当x=1000时,L=11000
因此,当销售商一次订购500个零件时,该厂获得的利润是6000元;
如果订购1000个,利润是11000元
【解析】(1)由题意设每个零件的实际出厂价恰好降为51元时,一次订购量为x0个,则 ![]() 因此,当一次订购量为550个时,每个零件的实际出厂价恰好降为51元;(2)前100件单价为P,当进货件数大于等于550件时,P=51,则当100<x<550时,
因此,当一次订购量为550个时,每个零件的实际出厂价恰好降为51元;(2)前100件单价为P,当进货件数大于等于550件时,P=51,则当100<x<550时, ![]() 得到P为分段函数,写出解析式即可;(3)设销售商的一次订购量为x个时,工厂获得的利润为L元,表示出L与x的函数关系式,然后令x=500,1000即可得到对应的利润.
得到P为分段函数,写出解析式即可;(3)设销售商的一次订购量为x个时,工厂获得的利润为L元,表示出L与x的函数关系式,然后令x=500,1000即可得到对应的利润.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x﹣alnx(a∈R)
(1)当a=2时,求曲线y=f(x)在点A(1,f(1))处的切线方程;
(2)求函数f(x)的极值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=sin(ωx+φ)(ω>0,|φ|< ![]() )的最小正周期是π,若其图象向右平移
)的最小正周期是π,若其图象向右平移 ![]() 个单位后得到的函数为奇函数,则函数f(x)的图象( )
个单位后得到的函数为奇函数,则函数f(x)的图象( )
A.关于点 ![]() 对称
对称
B.关于x= ![]() 对称
对称
C.关于点( ![]() ,0)对称
,0)对称
D.关于x= ![]() 对称
对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】求满足下列条件的直线方程:
(1)求经过直线l1:x+3y﹣3=0和l2:x﹣y+1=0的交点,且平行于直线2x+y﹣3=0的直线l的方程;
(2)已知直线l1:2x+y﹣6=0和点A(1,﹣1),过点A作直线l与l1相交于点B,且|AB|=5,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在(﹣∞,+∞)上的偶函数,且在(﹣∞,0]上是增函数,设a=f(log47),b=f(log ![]() 3),c=f(21.6),则a,b,c的大小关系是( )
3),c=f(21.6),则a,b,c的大小关系是( )
A.c<a<b
B.c<b<a
C.b<c<a
D.a<b<c
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合![]() 为集合
为集合![]() 的
的![]() 个非空子集,这
个非空子集,这![]() 个集合满足:①从中任取
个集合满足:①从中任取![]() 个集合都有
个集合都有![]()
![]()
![]() 成立;②从中任取
成立;②从中任取![]() 个集合都有
个集合都有![]()
![]() 成立.
成立.
(Ⅰ)若![]() ,
, ![]() ,
, ![]() ,写出满足题意的一组集合
,写出满足题意的一组集合![]() ;
;
(Ⅱ)若![]() ,
, ![]() ,写出满足题意的一组集合
,写出满足题意的一组集合![]() 以及集合
以及集合![]() ;
;
(Ⅲ) 若![]() ,
, ![]() ,求集合
,求集合![]() 中的元素个数的最小值.
中的元素个数的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com