
【题目】(本小题满分13分,(Ⅰ)小问5分,(Ⅱ)小问8分.)
甲、乙、丙三人按下面的规则进行乒乓球比赛:第一局由甲、乙参加而丙轮空,以后每一局由前一局的获胜者与轮空者进行比赛,而前一局的失败者轮空.比赛按这种规则一直进行到其中一人连胜两局或打满6局时停止.设在每局中参赛者胜负的概率均为![]() ,且各局胜负相互独立.求:(Ⅰ)打满3局比赛还未停止的概率;(Ⅱ)比赛停止时已打局数
,且各局胜负相互独立.求:(Ⅰ)打满3局比赛还未停止的概率;(Ⅱ)比赛停止时已打局数![]() 的分别列与期望E
的分别列与期望E![]() .
.
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (
(![]() )的左顶点为A,离心率为
)的左顶点为A,离心率为![]() ,点
,点![]() 在椭圆C上.
在椭圆C上.
(1)求椭圆C的方程;
(2)若直线![]() (
(![]() )与椭圆C交于E,F两点,直线
)与椭圆C交于E,F两点,直线![]() ,
,![]() 分别与y轴交于点M,N,求证:在x轴上存在点P,使得无论非零实数k怎样变化,以
分别与y轴交于点M,N,求证:在x轴上存在点P,使得无论非零实数k怎样变化,以![]() 为直径的圆都必过点P,并求出点P的坐标.
为直径的圆都必过点P,并求出点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.若等比数列![]() 的前
的前![]() 项和为
项和为![]() ,则
,则![]() ,
,![]() ,
,![]() 也成等比数列.
也成等比数列.
B.命题“若![]() 为
为![]() 的极值点,则
的极值点,则![]() ”的逆命题是真命题.
”的逆命题是真命题.
C.“![]() 为真命题”是“
为真命题”是“![]() 为真命题”的充分不必要条件.
为真命题”的充分不必要条件.
D.命题“![]() ,使得
,使得![]() ”的否定是:“
”的否定是:“![]() ,
,![]() ”.
”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 经过
经过![]() 两点,
两点,![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设动直线![]() 与椭圆
与椭圆![]() 有且仅有一个公共点,且与圆
有且仅有一个公共点,且与圆![]() 相交于
相交于![]() 两点,试问直线
两点,试问直线![]() 与
与![]() 的斜率之积
的斜率之积![]() 是否为定值?若是,求出该定值;若不是,说明理由.
是否为定值?若是,求出该定值;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中央政府为了对应因人口老龄化而造成的劳动力短缺等问题,拟定出台“延迟退休年龄政策”,为了了解人们对“延迟退休年龄政策”的态度,责成人社部进行调研,人社部从网上年龄在15~65的人群中随机调查50人,调查数据的频率分布直方图和支持“延迟退休”的人数与年龄的统计结果如下:
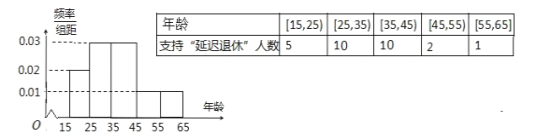
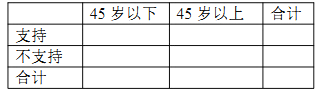
(1)由以上统计数据填下面2×2列联表,并问是否有90%的把握认为以45岁为分界点对“延迟退休年龄政策”的支持度有差异:
(2)若从年龄在![]() 的被调查人中随机选取两人进行调查,求选中的2人中恰有1人支持“延迟退休”的概率.
的被调查人中随机选取两人进行调查,求选中的2人中恰有1人支持“延迟退休”的概率.
参考数据:
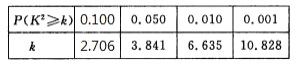
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学德育处为了解全校学生的上网情况,在全校随机抽取了40名学生(其中男、女生人数各占一半)进行问卷调查,并进行了统计,按男、女分为两组,再将每组学生的月上网次数分为5组:![]() ,得到如图所示的频率分布直方图.
,得到如图所示的频率分布直方图.
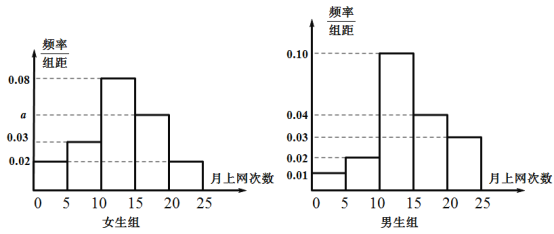
(1)写出女生组频率分布直方图中![]() 的值;
的值;
(2)求抽取的40名学生中月上网次数不少于15的学生人数;
(3)在抽取的40名学生中从月上网次数不少于20的学生中随机抽取3人,并用![]() 表示随机抽取的3人中男生的人数,求
表示随机抽取的3人中男生的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱柱ABCD﹣A1B1C1D1中,∠BAD=∠BCD=90°,∠ADC=60°且AD=CD,BB1⊥平面ABCD,BB1=2AB=2.
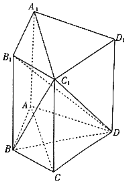
(1)证明:AC⊥B1D.
(2)求BC1与平面B1C1D所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了对某种商品进行合理定价,需了解该商品的月销售量![]() (单位:万件)与月销售单价
(单位:万件)与月销售单价![]() (单位:元/件)之间的关系,对近
(单位:元/件)之间的关系,对近![]() 个月的月销售量
个月的月销售量![]() 和月销售单价
和月销售单价![]()
![]() 数据进行了统计分析,得到一组检测数据如表所示:
数据进行了统计分析,得到一组检测数据如表所示:
月销售单价 |
|
|
|
|
|
|
月销售量 |
|
|
|
|
|
|
(1)若用线性回归模型拟合![]() 与
与![]() 之间的关系,现有甲、乙、丙三位实习员工求得回归直线方程分别为:
之间的关系,现有甲、乙、丙三位实习员工求得回归直线方程分别为:![]() ,
,![]() 和
和![]() ,其中有且仅有一位实习员工的计算结果是正确的.请结合统计学的相关知识,判断哪位实习员工的计算结果是正确的,并说明理由;
,其中有且仅有一位实习员工的计算结果是正确的.请结合统计学的相关知识,判断哪位实习员工的计算结果是正确的,并说明理由;
(2)若用![]() 模型拟合
模型拟合![]() 与
与![]() 之间的关系,可得回归方程为
之间的关系,可得回归方程为![]() ,经计算该模型和(1)中正确的线性回归模型的相关指数
,经计算该模型和(1)中正确的线性回归模型的相关指数![]() 分别为
分别为![]() 和
和![]() ,请用
,请用![]() 说明哪个回归模型的拟合效果更好;
说明哪个回归模型的拟合效果更好;
(3)已知该商品的月销售额为![]() (单位:万元),利用(2)中的结果回答问题:当月销售单价为何值时,商品的月销售额预报值最大?(精确到
(单位:万元),利用(2)中的结果回答问题:当月销售单价为何值时,商品的月销售额预报值最大?(精确到![]() )
)
参考数据:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,过点
,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() 交函数
交函数![]() 图象于点
图象于点![]() ,以
,以![]() 为切点作函数
为切点作函数![]() 图象的切线交
图象的切线交![]() 轴于点
轴于点![]() ,再过
,再过![]() 作
作![]() 轴的垂线
轴的垂线![]() 交函数
交函数![]() 图象于点
图象于点![]() ,
,![]() ,以此类推得点
,以此类推得点![]() ,记
,记![]() 的横坐标为
的横坐标为![]() ,
,![]() .
.
(1)证明数列![]() 为等比数列并求出通项公式;
为等比数列并求出通项公式;
(2)设直线![]() 与函数
与函数![]() 的图象相交于点
的图象相交于点![]() ,记
,记![]() (其中
(其中![]() 为坐标原点),求数列
为坐标原点),求数列![]() 的前
的前![]() 项和
项和![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com