
【题目】在等比数列{an}中,公比q≠1,等差数列{bn}满足b1=a1=3,b4=a2 , b13=a3 .
(1)求数列{an}与{bn}的通项公式;
(2)记cn=(﹣1)nbn+an , 求数列{cn}的前n项和Sn .
【答案】
(1)解:设等比数列{an}的公比为q(q≠1),等差数列{bn}的公差为d.
由已知得: ![]() ,b1=3,b4=3+3d,b13=3+12d,
,b1=3,b4=3+3d,b13=3+12d,
所以 ![]() 或 q=1(舍去),
或 q=1(舍去),
所以,此时 d=2,
所以, ![]() ,bn=2n+1;
,bn=2n+1;
(2)解:由题意得: ![]() ,
,
Sn=c1+c2+…+cn=(﹣3+5)+(﹣7+9)+…+(﹣1)n﹣1(2n﹣1)+(﹣1)n(2n+1)+3+32+…+3n,
当n为偶数时, ![]() ,
,
当n为奇数时, ![]() ,
,
所以, 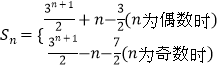 .
.
【解析】(1)设等比数列{an}的公比为q(q≠1),等差数列{bn}的公差为d,根据b1=a1 , b4=a2 , b13=a3及等差、等比数列的通项公式列关于q,d的方程组解出即得q,d,再代入通项公式即可;(2)由(1)知 ![]() ,Sn=c1+c2+…+cn=(﹣3+5)+(﹣7+9)+…+(﹣1)n﹣1(2n﹣1)+(﹣1)n(2n+1)+3+32+…+3n , 分n为奇数、偶数两种情况讨论即可;
,Sn=c1+c2+…+cn=(﹣3+5)+(﹣7+9)+…+(﹣1)n﹣1(2n﹣1)+(﹣1)n(2n+1)+3+32+…+3n , 分n为奇数、偶数两种情况讨论即可;


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在以原点为极点,
为参数),在以原点为极点, ![]() 轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的倾斜角;
的倾斜角;
(2)设点![]() ,直线
,直线![]() 和曲线
和曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥![]() 中,
中, ![]() 平面
平面![]() 是
是![]() 的中点,
的中点, ![]() 是
是![]() 上的点且
上的点且![]() 为
为![]() 边
边![]() 上的高.
上的高.

(1)证明: ![]() 平面
平面![]() ;
;
(2)若![]() ,求三棱锥
,求三棱锥![]() 的体积;
的体积;
(3)在线段![]() 上是否存在这样一点
上是否存在这样一点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,说出
?若存在,说出![]() 点的位置.
点的位置.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是椭圆
是椭圆![]() 上关于原点
上关于原点![]() 对称的任意两点,且点
对称的任意两点,且点![]() 都不在
都不在![]() 轴上.
轴上.
(1)若![]() ,求证: 直线
,求证: 直线![]() 和
和![]() 的斜率之积为定值;
的斜率之积为定值;
(2)若椭圆长轴长为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,设
上,设![]() 是椭圆上异于点
是椭圆上异于点![]() 的任意两点,且
的任意两点,且![]() .问直线
.问直线![]() 是否过一个定点?若过定点,求出该定点坐标;若不过定点,请说明理由.
是否过一个定点?若过定点,求出该定点坐标;若不过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
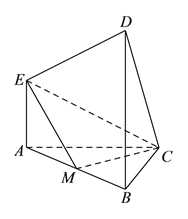
【题目】在如图所示的多面体中, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,且
,且![]() ,
, ![]() 是
是![]() 的中点.
的中点.
(Ⅰ)求证: ![]() .
.
(Ⅱ)求平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
(Ⅲ)在棱![]() 上是否存在一点
上是否存在一点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成的角是
所成的角是![]() .若存在,指出点
.若存在,指出点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某货轮匀速行驶在相距![]() 海里的甲、乙两地间运输货物,运输成本由燃料费用和其他费用组成.已知该货轮每小时的燃料费用与其航行速度的平方成正比(比例系数为
海里的甲、乙两地间运输货物,运输成本由燃料费用和其他费用组成.已知该货轮每小时的燃料费用与其航行速度的平方成正比(比例系数为![]() ),其他费用为每小时
),其他费用为每小时![]() 元,且该货轮的最大航行速度为
元,且该货轮的最大航行速度为![]() 海里/小时.
海里/小时.
(1)请将从甲地到乙地的运输成本![]() (元)表示为航行速度
(元)表示为航行速度![]() (海里/小时)的函数;
(海里/小时)的函数;
(2)要使从甲地到乙地的运输成本最少,该货轮应以多大的航行速度行驶?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com