
如图示,在底面为直角梯形的四棱椎P
ABCD中,AD//BC,ÐABC= 900, PA^平面ABCD,PA= 4,AD= 2,AB=2 ,BC
= 6.
,BC
= 6.

(1)求证:BD^平面PAC ;
(2)求二面角A—PC—D的正切值;
(3)求点D到平面PBC的距离.
(1)见解析;(2)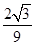 ;(3)
;(3)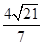
【解析】
试题分析:(1)三角形AOB中,由勾股定理得:BO^AC,即:BD^AC, 又BD^PA,ACÇ PA=A,由线面垂直判定定理可得BD^平面PAC;(2)先作出二面角的平面角,然后在直角三角形中求出正切值;(3)利用等积法,由VD—PBC = VP—BDC即可求出点D到平面PBC的距离.
试题解析:解:(1)令BD与AC相交于点O,不难求得:AC=4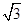 ,BD=
4
,BD=
4
由DAOD~DBOC得:BO=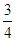 ×4= 3;AO=
×4= 3;AO=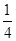 ×4
×4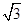 =
=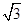 ;
;
\ BO2+AO2 = (3)2+(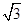 )2=
12= AB2
)2=
12= AB2
\由勾股定理得:BO^AC,即:BD^AC, 又BD^PA,ACÇ PA=A,
\ BD^平面PAC 3分
(2)由(1)知:DO^平面PAC,过O作OH^PC于H,连DH,则DH^PC
则ÐDHO就是二面角A—PC—D的平面角, DO=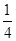 ×BD =
×BD =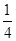 ×4=1 ,
×4=1 ,
CO=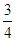 ×AC=
×AC=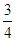 ×4
×4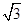 =3
=3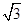 ,
由RtDPAC~RtDOHC得:
,
由RtDPAC~RtDOHC得: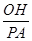 =
=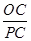 ,又PC=
,又PC= 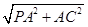 =
8, OH=
=
8, OH= .tanÐDHO=
.tanÐDHO=  =
=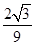 .
7分
.
7分
(3)由VD—PBC = VP—BDC可得:h=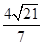 .
10分
.
10分
考点:1.线面垂直的判定;2.二面角的求法;3.点到平面的距离求法


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com