
ЎҫМвДҝЎҝҙУДіөзЧУЙМОсЖҪМЁЛж»ъійИЎБЛ1000О»НшЙП№әОпХЯЈЁДкПы·С¶јҙпөҪ2000ФӘЈ©Ј¬Іў¶ФЛыГЗөДДкБдҪшРРБЛөчІйЈ¬НіјЖЗйҝцИзПВұнЛщКҫЈә
ДкБд |
|
|
|
|
|
|
ИЛКэ | 100 | 150 | 400 | 200 | 100 | 50 |
ёГөзЧУЙМОсЖҪМЁҪ«ДкБдФЪ![]() өДИЛИә¶ЁТеОӘПы·СЦчБҰҫьЈ¬ЖдЛьДкБд¶О¶ЁТеОӘПы·СЗұБҰҫь.
өДИЛИә¶ЁТеОӘПы·СЦчБҰҫьЈ¬ЖдЛьДкБд¶О¶ЁТеОӘПы·СЗұБҰҫь.
ЈЁ1Ј©ИфёГөзЧУЙМОсЖҪМЁ№І10НтО»НшЙП№әОпХЯЈ¬КФ№АјЖПы·СЦчБҰҫьөДИЛКэЈ»
ЈЁ2Ј©ОӘБЛ№ДАшПы·СЗұБҰҫьПы·СЈ¬ёГЖҪМЁҫц¶Ё¶ФДкПы·СҙпөҪ2000ФӘөД№әОпХЯ·ў·ЕҙъҪрИҜЈ¬Пы·СЦчБҰҫьГҝИЛ·ў·Е100ФӘЈ¬Пы·СЗұБҰҫьГҝИЛ·ў·Е200ФӘ.ПЦІЙУГ·ЦІгійСщЈЁ°ҙПы·СЦчБҰҫьУлПы·СЗұБҰҫь·ЦІгЈ©өД·ҪКҪҙУІОУлөчІйөД1000О»НшЙП№әОпХЯЦРійИЎ10ИЛЈ¬ІўФЪХв10ИЛЦРЛж»ъійИЎ3ИЛҪшРР»Ш·ГЈ¬ЗуХв3ИЛ»сөГҙъҪрИҜЧЬҪр¶о![]() ЈЁөҘО»ЈәФӘЈ©өД·ЦІјБРј°КэС§ЖЪНы.
ЈЁөҘО»ЈәФӘЈ©өД·ЦІјБРј°КэС§ЖЪНы.
Ўҫҙр°ёЎҝЈЁ1Ј©![]() НтЈ»ЈЁ2Ј©·ЦІјБРјыҪвОцЈ¬ЖЪНыОӘ
НтЈ»ЈЁ2Ј©·ЦІјБРјыҪвОцЈ¬ЖЪНыОӘ![]() ФӘ.
ФӘ.
ЎҫҪвОцЎҝ
ЈЁ1Ј©ёщҫЭЦұ·ҪНјХТіцДкБд·ЦІјФЪ![]() өДЖөВКФЩіЛТФ10НтөГҪвЈ»
өДЖөВКФЩіЛТФ10НтөГҪвЈ»
ЈЁ2Ј©ёщҫЭПы·СЦчБҰҫьУлПы·СЗұБҰҫьИЛИәөДұИАэ№ШПөөГіцИЛКэұИЈ¬ ФЩёщҫЭі¬јёәО·ЦІјөДёЕВК№«КҪөГіц·ЦІјБРәНКэС§ЖЪНыЈ®
ҪвЈәЈЁ1Ј©УЙұнҝЙЦӘДкБд·ЦІјФЪ![]() өДЖөВКОӘ
өДЖөВКОӘ![]() Ј¬
Ј¬
№КПы·СЦчБҰҫьөДИЛКэФјОӘ![]() Нт.
Нт.
ЈЁ2Ј©УЙМвҝЙЦӘХв10ИЛЦРУР6ИЛКфУЪПы·СЦчБҰҫьЈ¬4ИЛКфУЪПы·СЗұБҰҫьЈ¬Фт![]() өДЛщУРҝЙДЬИЎЦөОӘ300Ј¬400Ј¬500,600Ј¬
өДЛщУРҝЙДЬИЎЦөОӘ300Ј¬400Ј¬500,600Ј¬
![]() Ј¬
Ј¬![]() Ј¬
Ј¬
![]() Ј¬
Ј¬![]() Ј¬
Ј¬
№К![]() өД·ЦІјБРОӘ
өД·ЦІјБРОӘ
| 300 | 400 | 500 | 600 |
|
|
|
|
|
![]()
![]()
![]() ФӘ.
ФӘ.



| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝПВБРЛө·ЁЦРЈ¬ХэИ·өДёцКэКЗЈЁ Ј©
ўЩA=![]() өДЧУјҜУР
өДЧУјҜУР![]() ёцЈ»
ёцЈ»
ўЪГьМвЎ°![]() ЎұөД·с¶ЁКЗЎ°
ЎұөД·с¶ЁКЗЎ°![]() К№өГ
К№өГ![]() ЎұЈ»
ЎұЈ»
ўЫЎ°![]() ЎұКЗЎ°әҜКэ
ЎұКЗЎ°әҜКэ![]() ИЎөГЧоҙуЦөЎұөДід·ЦІ»ұШТӘМхјюЈ»
ИЎөГЧоҙуЦөЎұөДід·ЦІ»ұШТӘМхјюЈ»
ўЬёщҫЭ¶ФКэ¶ЁТеЈ¬¶ФКэКҪ![]() »ҜОӘЦёКэКҪ
»ҜОӘЦёКэКҪ![]() Ј»
Ј»
ўЭИф![]() Ј¬Фт
Ј¬Фт![]() өДИЎЦө·¶О§ОӘ
өДИЎЦө·¶О§ОӘ![]() Ј»
Ј»
ўЮ![]() .
.
A.![]() ёцB.
ёцB.![]() ёцC.
ёцC.![]() ёцD.
ёцD.![]() ёц
ёц
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИфәҜКэ![]() КЗ¶ЁТеФЪ
КЗ¶ЁТеФЪ![]() ЙПөДЖжәҜКэЈ¬ЗТөұ
ЙПөДЖжәҜКэЈ¬ЗТөұ![]() КұЈ¬
КұЈ¬![]() .
.
ЈЁўсЈ©Иф![]() Ј¬ЗуәҜКэ
Ј¬ЗуәҜКэ![]() өДҪвОцКҪЈ»
өДҪвОцКҪЈ»
ЈЁўтЈ©Иф![]() Ј¬·ҪіМ
Ј¬·ҪіМ![]() ЦБЙЩУРБҪёцІ»өИөДҪвЈ¬Зу
ЦБЙЩУРБҪёцІ»өИөДҪвЈ¬Зу![]() өДИЎЦөјҜәПЈ»
өДИЎЦөјҜәПЈ»
ЈЁўуЈ©ИфәҜКэ![]() ОӘ
ОӘ![]() ЙПөДөҘөчјхәҜКэЈ¬
ЙПөДөҘөчјхәҜКэЈ¬
ўЩЗу![]() өДИЎЦө·¶О§Ј»
өДИЎЦө·¶О§Ј»
ўЪИфІ»өИКҪ![]() іЙБўЈ¬ЗуКөКэ
іЙБўЈ¬ЗуКөКэ![]() өДИЎЦөјҜәП.
өДИЎЦөјҜәП.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝЙи¶ЁТеФЪ![]() ЙПөДәҜКэ
ЙПөДәҜКэ![]() Ўў
Ўў![]() әН
әН![]() Ј¬ВъЧг
Ј¬ВъЧг![]() Ј¬ЗТ¶ФИОТвКөКэ
Ј¬ЗТ¶ФИОТвКөКэ![]() Ўў
Ўў![]() ЈЁ
ЈЁ![]() Ј©Ј¬әгУР
Ј©Ј¬әгУР![]() іЙБў.
іЙБў.
ўЕКФРҙ іцТ»ЧйВъЧгМхјюөДҫЯМеөД![]() әН
әН![]() Ј¬К№
Ј¬К№![]() ОӘФцәҜКэЈ¬
ОӘФцәҜКэЈ¬![]() ОӘјхәҜКэЈ¬ө«
ОӘјхәҜКэЈ¬ө«![]() ОӘФцәҜКэ.
ОӘФцәҜКэ.
ўЖЕР¶ППВБРБҪёцГьМвөДХжјЩЈ¬ІўЛөГчАнУЙ.
ГьМв1Ј©ЈәИф![]() ОӘФцәҜКэЈ¬Фт
ОӘФцәҜКэЈ¬Фт![]() ОӘФцәҜКэЈ»
ОӘФцәҜКэЈ»
ГьМв2Ј©ЈәИф![]() ОӘФцәҜКэЈ¬Фт
ОӘФцәҜКэЈ¬Фт![]() ОӘФцәҜКэ.
ОӘФцәҜКэ.
ўЗТСЦӘ![]() Ј¬РҙіцТ»ЧйВъЧгМхјюөДҫЯМеөД
Ј¬РҙіцТ»ЧйВъЧгМхјюөДҫЯМеөД![]() әН
әН![]() Ј¬ЗТ
Ј¬ЗТ![]() ОӘ·ЗіЈЦөәҜКэЈ¬ІўЛөГчАнУЙ.
ОӘ·ЗіЈЦөәҜКэЈ¬ІўЛөГчАнУЙ.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝјЗЗъПЯfЈЁxЈ©ЈҪx©Ғe©ҒxЙПИОТвТ»өгҙҰөДЗРПЯОӘЦұПЯlЈәyЈҪkx+bЈ¬Фтk+bөДЦөІ»ҝЙДЬОӘЈЁЎЎЎЎЈ©
A. ![]() B. 1 C. 2 D. 3
B. 1 C. 2 D. 3
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝ![]() КРКөК©И«УтВГУОЈ¬Ҫ«ПзҙеВГУО№«В·ҪЁЙиУлМШЙ«МпФ°Пзҙе·ўХ№ҪбәПЈ¬ҫ«РДҙтФмИ«іӨ365№«АпөДЎ°1әЕ№«В·ЎұЈ¬¶ФДЪҙ®БӘЗшУтДЪЦчТӘҫ°Зшҫ°өгәНЧФИ»ҙеЈ¬¶ФНвНЁҙпЦЬұЯПШЈЁКРЈ©Ј¬ТФВ·Тэҫ°ЎўОӘҫ°ҙ®ПЯЈ¬РОіЙТ»ёцЎ°ҙу»·РЎИҰЎўДЪБ¬НвТэЎұөДВ·НшМеПө.ИзҪсөДЎ°1әЕ№«В·ЎұЈ¬І»ҪціЙОӘёГКРВГУОТөөДЎ°СХЦөөЈөұЎұЈ¬ёьіЙОӘНЖ¶ҜПзҙеХсРЛөДЎ°КөБҰөЈөұЎұЈ¬Е©ҙеҫУЧЎ»·ҫіИХТжёДЙЖЈ¬РВЕ©ҙеұрКыЛжҙҰҝЙјы.НјўЩКЗТ»¶°РВЕ©ҙеұрКыЈ¬ЛьУЙЙПІҝОЭ¶ҘәНПВІҝЦчМеБҪІҝ·ЦЧйіЙ.ИзНјўЪЈ¬ОЭ¶ҘУЙЛДЖВОЭГж№№іЙЈ¬ЖдЦРЗ°әуБҪЖВОЭГж
КРКөК©И«УтВГУОЈ¬Ҫ«ПзҙеВГУО№«В·ҪЁЙиУлМШЙ«МпФ°Пзҙе·ўХ№ҪбәПЈ¬ҫ«РДҙтФмИ«іӨ365№«АпөДЎ°1әЕ№«В·ЎұЈ¬¶ФДЪҙ®БӘЗшУтДЪЦчТӘҫ°Зшҫ°өгәНЧФИ»ҙеЈ¬¶ФНвНЁҙпЦЬұЯПШЈЁКРЈ©Ј¬ТФВ·Тэҫ°ЎўОӘҫ°ҙ®ПЯЈ¬РОіЙТ»ёцЎ°ҙу»·РЎИҰЎўДЪБ¬НвТэЎұөДВ·НшМеПө.ИзҪсөДЎ°1әЕ№«В·ЎұЈ¬І»ҪціЙОӘёГКРВГУОТөөДЎ°СХЦөөЈөұЎұЈ¬ёьіЙОӘНЖ¶ҜПзҙеХсРЛөДЎ°КөБҰөЈөұЎұЈ¬Е©ҙеҫУЧЎ»·ҫіИХТжёДЙЖЈ¬РВЕ©ҙеұрКыЛжҙҰҝЙјы.НјўЩКЗТ»¶°РВЕ©ҙеұрКыЈ¬ЛьУЙЙПІҝОЭ¶ҘәНПВІҝЦчМеБҪІҝ·ЦЧйіЙ.ИзНјўЪЈ¬ОЭ¶ҘУЙЛДЖВОЭГж№№іЙЈ¬ЖдЦРЗ°әуБҪЖВОЭГж![]() әН
әН![]() КЗИ«өИөДөИСьМЭРОЈ¬ЧуУТБҪЖВОЭГж
КЗИ«өИөДөИСьМЭРОЈ¬ЧуУТБҪЖВОЭГж![]() әН
әН![]() КЗИ«өИөДИэҪЗРО.өг
КЗИ«өИөДИэҪЗРО.өг![]() ФЪЖҪГж
ФЪЖҪГж![]() әН
әН![]() ЙПөДЙдУ°·ЦұрОӘ
ЙПөДЙдУ°·ЦұрОӘ![]() ЈЁјҙЈә
ЈЁјҙЈә![]() ЖҪГж
ЖҪГж![]() Ј¬ҙ№ЧгОӘ
Ј¬ҙ№ЧгОӘ![]() Ј»
Ј»![]() Ј¬ҙ№ЧгОӘ
Ј¬ҙ№ЧгОӘ![]() Ј©.ТСЦӘ
Ј©.ТСЦӘ![]() Ј¬МЭРО
Ј¬МЭРО![]() өДГж»эКЗ
өДГж»эКЗ![]() Гж»эөД2.2ұ¶.
Гж»эөД2.2ұ¶.![]() .
.

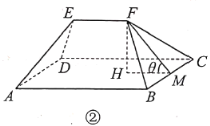
ЈЁ1Ј©өұ![]() КұЈ¬ЗуОЭ¶ҘГж»эөДҙуРЎЈ»
КұЈ¬ЗуОЭ¶ҘГж»эөДҙуРЎЈ»
ЈЁ2Ј©ЗуОЭ¶ҘГж»э![]() №ШУЪ
№ШУЪ![]() өДәҜКэ№ШПөКҪЈ»
өДәҜКэ№ШПөКҪЈ»
ЈЁ3Ј©ТСЦӘЙПІҝОЭ¶ҘФмјЫУлОЭ¶ҘГж»эіЙХэұИЈ¬ұИАэПөКэОӘ![]() ЈЁ
ЈЁ![]() ОӘХэөДіЈКэЈ©Ј¬ПВІҝЦчМеФмјЫУлЖдёЯ¶ИіЙХэұИЈ¬ұИАэПөКэОӘ
ОӘХэөДіЈКэЈ©Ј¬ПВІҝЦчМеФмјЫУлЖдёЯ¶ИіЙХэұИЈ¬ұИАэПөКэОӘ![]() .ПЦУыФмТ»¶°ЙПЎўПВЧЬёЯ¶ИОӘ
.ПЦУыФмТ»¶°ЙПЎўПВЧЬёЯ¶ИОӘ![]() өДұрКыЈ¬КФОКЈәөұ
өДұрКыЈ¬КФОКЈәөұ![]() ОӘәОЦөКұЈ¬ЧЬФмјЫЧоөНЈҝ
ОӘәОЦөКұЈ¬ЧЬФмјЫЧоөНЈҝ
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘәҜКэ![]() ЈЁ
ЈЁ![]() Ј©Ј¬
Ј©Ј¬![]() .
.
ЈЁ1Ј©Иф![]() өДНјПуФЪ
өДНјПуФЪ![]() ҙҰөДЗРПЯЗЎәГТІКЗ
ҙҰөДЗРПЯЗЎәГТІКЗ![]() НјПуөДЗРПЯ.
НјПуөДЗРПЯ.
ўЩЗуКөКэ![]() өДЦөЈ»
өДЦөЈ»
ўЪИф·ҪіМ![]() ФЪЗшјд
ФЪЗшјд![]() ДЪУРОЁТ»КөКэҪвЈ¬ЗуКөКэ
ДЪУРОЁТ»КөКэҪвЈ¬ЗуКөКэ![]() өДИЎЦө·¶О§.
өДИЎЦө·¶О§.
ЈЁ2Ј©өұ![]() КұЈ¬ЗуЦӨЈә¶ФУЪЗшјд
КұЈ¬ЗуЦӨЈә¶ФУЪЗшјд![]() ЙПөДИОТвБҪёцІ»ПаөИөДКөКэ
ЙПөДИОТвБҪёцІ»ПаөИөДКөКэ![]() Ј¬
Ј¬ ![]() Ј¬¶јУР
Ј¬¶јУР![]() іЙБў.
іЙБў.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘНЦФІ![]() ЦРРДФЪФӯөгЈ¬Ҫ№өгФЪЧшұкЦбЙПЈ¬ЦұПЯ
ЦРРДФЪФӯөгЈ¬Ҫ№өгФЪЧшұкЦбЙПЈ¬ЦұПЯ![]() УлНЦФІ
УлНЦФІ![]() ФЪөЪТ»ПуПЮДЪөДҪ»өгКЗ
ФЪөЪТ»ПуПЮДЪөДҪ»өгКЗ![]() Ј¬өг
Ј¬өг![]() ФЪ
ФЪ![]() ЦбЙПөДЙдУ°ЗЎәГКЗНЦФІ
ЦбЙПөДЙдУ°ЗЎәГКЗНЦФІ![]() өДУТҪ№өг
өДУТҪ№өг![]() Ј¬НЦФІ
Ј¬НЦФІ![]() БнТ»ёцҪ№өгКЗ
БнТ»ёцҪ№өгКЗ![]() Ј¬ЗТ
Ј¬ЗТ![]() .
.
ЈЁ1Ј©ЗуНЦФІ![]() өД·ҪіМЈ»
өД·ҪіМЈ»
ЈЁ2Ј©ЦұПЯ![]() №эөг
№эөг![]() Ј¬ЗТУлНЦФІ
Ј¬ЗТУлНЦФІ![]() Ҫ»УЪ
Ҫ»УЪ![]() БҪөгЈ¬Зу
БҪөгЈ¬Зу![]() өДДЪЗРФІГж»эөДЧоҙуЦө.
өДДЪЗРФІГж»эөДЧоҙуЦө.
Ійҝҙҙр°ёәНҪвОц>>
°Щ¶ИЦВРЕ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com