练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，在等腰三角形ABC中，已知AB=AC=1，A=120°，E，F分别是边AB，AC上的点，且 ， ，其中m，n∈（0，1）．若EF，BC的中点分别为M，N，且m+4n=1，则 的最小值为 ．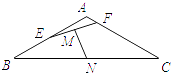

    【答案】
    【解析】解：连接AM、AN， ∵等腰三角形ABC中，AB=AC=1，A=120°，
    ∴ =| || |cos120°=﹣
    ∵AM是△AEF的中线，
    ∴ = （ ）= （ + ）
    同理，可得 = （ + ），
    由此可得 = ﹣ = （1﹣m） + （1﹣n）
    ∴ =[ （1﹣m） + （1﹣n） ]2= （1﹣m）2+ （1﹣m）（1﹣n） + （1﹣n）2
    = （1﹣m）2﹣ （1﹣m）（1﹣n）+ （1﹣n）2 ，
    ∵m+4n=1，可得1﹣m=4n
    ∴代入上式得 = ×（4n）2﹣ ×4n（1﹣n）+ （1﹣n）2= n2﹣ n+
    ∵m，n∈（0，1），
    ∴当n= 时， 的最小值为 ，此时 的最小值为 ．
    所以答案是：

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）= 为偶函数
    （1）求实数a的值；
    （2）记集合E={y|y=f（x），x∈{﹣1，1，2}}，λ=lg22+lg2lg5+lg5﹣ ，判断λ与E的关系；
    （3）当x∈[ ， ]（m＞0，n＞0）时，若函数f（x）的值域[2﹣3m，2﹣3n]，求实数m，n值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

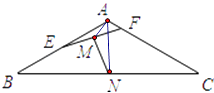
    【题目】在如图所示的几何体中，四边形ABCD是等腰梯形，AB∥CD，∠DAB=60°，FC⊥平面ABCD，AE⊥BD，CB=CD=CF．
    （Ⅰ）求证：BD⊥平面AED；
    （Ⅱ）求二面角F﹣BD﹣C的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了在夏季降温和冬季供暖时减少能源损耗，房屋的屋顶和外墙需要建造隔热层．某幢建筑物要建造可使用20年的隔热层，每厘米厚的隔热层建造成本为6万元．该建筑物每年的能源消耗费用C（单位：万元）与隔热层厚度x（单位：cm）满足关系：C（x）= （0≤x≤10），若不建隔热层，每年能源消耗费用为8万元．设f（x）为隔热层建造费用与20年的能源消耗费用之和．
    （1）求k的值及f（x）的表达式．
    （2）隔热层修建多厚时，总费用f（x）达到最小，并求最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

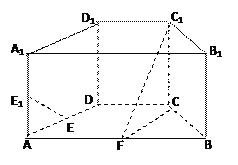
    【题目】如图，在直四棱柱ABCD-ABCD中，底面ABCD为等腰梯形，AB//CD，AB=4, BC=CD=2, AA=2, E、E、F分别是棱AD、AA、AB的中点。

    证明：（1）直线EE//平面FCC；

    （2）求二面角B-FC-C的余弦值。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某校在2016年的自主招生考试成绩中随机抽取100名学生的笔试成绩，被抽取学生的成绩均不低于160分，且低于185分，如图是按成绩分组得到的频率分布直方图．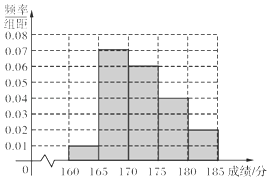

    （1）为了能选拔出优秀的学生，该校决定在笔试成绩较高的第3组、第4组、第5组中用分层抽样的方法抽取6名学生进入第二轮面试，求第3，4，5组每组各抽取多少名学生进入第二轮面试；
    （2）在（1）的前提下，学校决定在6名学生中随机抽取2名学生由考官A面试，求第4组至少有一名学生被考官A面试的概．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，“嫦娥一号”探月卫星沿地月转移轨道飞向月球，在月球附近一点P变轨进入以月球球心F为一个焦点的椭圆轨道Ⅰ绕月飞行，之后卫星在P点第二次变轨进入仍以F为一个焦点的椭圆轨道Ⅱ绕月飞行，最终卫星在P点第三次变轨进入以F为圆心的圆形轨道Ⅲ绕月飞行，若用2c1和2c2分别表示椭圆轨道Ⅰ和Ⅱ的焦距，用2a1和2a2分别表示椭圆轨道Ⅰ和Ⅱ的长轴的长，给出下列式子：
    ①a1+c1=a2+c2；②a1﹣c1=a2﹣c2；③c1a2＞a1c2；④ ．
    其中正确式子的序号是（ ）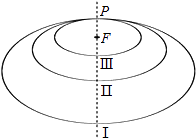

    A.①③
    B.②③
    C.①④
    D.②④

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知双曲线 的两个焦点为
    的曲线C上．
    （1）求双曲线C的方程；
    （2）记O为坐标原点，过点Q（0，2）的直线l与双曲线C相交于不同的两点E、F，若△OEF的面积为2 ，求直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】命题p：实数x满足x2﹣4ax+3a2＜0（其中a＞0），命题q：实数x满足
    （1）若a=1，且p∧q为真，求实数x的取值范围；
    （2）若￢p是￢q的充分不必要条件，求实数a的取值范围．

    查看答案和解析>>

    同步练习册答案