
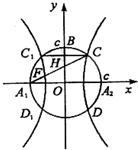
 ČçÍźŁŹŇÔA1ŁŹA2ÎŞ˝šľăľÄËŤÇúĎßEÓë°ëžśÎŞcľÄÔ˛OĎཝÓÚCŁŹDŁŹC1ŁŹD1ŁŹÁŹ˝ÓCC1ÓëOB˝ťÓÚľăHŁŹÇŇÓĐŁş
ČçÍźŁŹŇÔA1ŁŹA2ÎŞ˝šľăľÄËŤÇúĎßEÓë°ëžśÎŞcľÄÔ˛OĎཝÓÚCŁŹDŁŹC1ŁŹD1ŁŹÁŹ˝ÓCC1ÓëOB˝ťÓÚľăHŁŹÇŇÓĐŁş| OH |
| 3 |
| HB |
| A1F |
| FC |
| A1F |
| FC |
| OH |
| 3 |
| HB |
3+2
| ||
4+2
|
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
|
|
| x2 | ||||
1-
|
| y2 | ||||
|
| H |
| 3 |
| B |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
|
| b |
| a |
| b |
| a |
| b |
| a |
| 3 |
| c2 |
| a2 |
| b |
| a |
| 3 |
4+2
|
| 3 |
| F |
| C |
| c |
| 2 |
| ||
| 2 |
-c+
| ||
| 1+ŚË |
| ||||
| 1+ŚË |
| c(ŚË-2) |
| 2(1+ŚË) |
| ||
| 2(1+ŚË) |
|
| 3c2 |
| b2 |
| c2 |
| b2 |
| e2-4 |
| 3 |
| e2(ŚË-2)2 |
| 4(1+ŚË)2 |
| ŚË2 |
| 4(1+ŚË)2 |
| e2-1 |
| e2+2 |
3+2
| ||
6+2
|
1+
| ||
| 4 |
1+
| ||
| 4 |
| F |
| C |



| Äęźś | ¸ßÖĐżÎłĚ | Äęźś | łőÖĐżÎłĚ |
| ¸ßŇť | ¸ßŇťĂâˇŃżÎłĚÍĆźöŁĄ | łőŇť | łőŇťĂâˇŃżÎłĚÍĆźöŁĄ |
| ¸ßśţ | ¸ßśţĂâˇŃżÎłĚÍĆźöŁĄ | łőśţ | łőśţĂâˇŃżÎłĚÍĆźöŁĄ |
| ¸ßČý | ¸ßČýĂâˇŃżÎłĚÍĆźöŁĄ | łőČý | łőČýĂâˇŃżÎłĚÍĆźöŁĄ |
żĆÄżŁş¸ßÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
 ËćťúłéČĄÄł˛úơnźţŁŹ˛âľĂĆ䳤śČˇÖąđÎŞŇÔa1ŁŹa2ŁŹĄŁŹanŁŹÔňČçÍźËůĘžľÄłĚĐňżňÍźĘäłöľÄs=
ËćťúłéČĄÄł˛úơnźţŁŹ˛âľĂĆ䳤śČˇÖąđÎŞŇÔa1ŁŹa2ŁŹĄŁŹanŁŹÔňČçÍźËůĘžľÄłĚĐňżňÍźĘäłöľÄs=| a1+a2+a2+Ą+an |
| n |
| a1+a2+a2+Ą+an |
| n |
˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁş¸ßÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
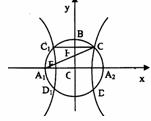
ČçÍźŁŹŇÔA1Ą˘A2ÎŞ˝š ľăľÄËŤÇúĎßEÓë°ëžśÎŞcľÄÔ˛OĎཝÓÚCĄ˘DĄ˘C1Ą˘D1ŁŹÁŹ˝ÓCC1ÓëOB˝ťÓÚľăHŁŹÇŇÓĐ![]() ĘÇÔ˛OÓë×řąęÖáľÄ˝ťľăŁŹcÎŞËŤÇúĎ߾İ뽚žŕ.
ĘÇÔ˛OÓë×řąęÖáľÄ˝ťľăŁŹcÎŞËŤÇúĎ߾İ뽚žŕ.
Ł¨1ŁŠľąc=1ĘąŁŹÇóËŤÇúĎßEľÄˇ˝łĚŁť
Ł¨2ŁŠĘÔÖ¤ŁşśÔČÎŇâŐýĘľĘýcŁŹËŤÇúĎßEľÄŔëĐÄÂĘÎŞłŁĘýŁť
Ł¨3ŁŠÁŹ˝ÓA1CŁŹÓëËŤÇúĎßE˝ťÓÚľăFŁŹĘǡń´ćÔÚĘľĘý![]() ŁŹĘš
ŁŹĘš![]() şăłÉÁ˘ŁżČô´ćÔÚŁŹĘÔÇółö
şăłÉÁ˘ŁżČô´ćÔÚŁŹĘÔÇółö![]() ľÄÖľŁťČô˛ť´ćÔÚŁŹÇëËľĂ÷ŔíÓÉ.
ľÄÖľŁťČô˛ť´ćÔÚŁŹÇëËľĂ÷ŔíÓÉ.
˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁş¸ßÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
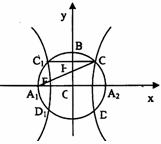
ČçÍźŁŹŇÔA1Ą˘A2ÎŞ˝š ľăľÄËŤÇúĎßEÓë°ëžśÎŞcľÄÔ˛OĎཝÓÚCĄ˘DĄ˘C1Ą˘D1ŁŹÁŹ˝ÓCC1ÓëOB˝ťÓÚľăHŁŹÇŇÓĐ![]() ĘÇÔ˛OÓë×řąęÖáľÄ˝ťľăŁŹcÎŞËŤÇúĎ߾İ뽚žŕ.
ĘÇÔ˛OÓë×řąęÖáľÄ˝ťľăŁŹcÎŞËŤÇúĎ߾İ뽚žŕ.
Ł¨1ŁŠľąc=1ĘąŁŹÇóËŤÇúĎßEľÄˇ˝łĚŁť
Ł¨2ŁŠĘÔÖ¤ŁşśÔČÎŇâŐýĘľĘýcŁŹËŤÇúĎßEľÄŔëĐÄÂĘÎŞłŁĘýŁť
Ł¨3ŁŠÁŹ˝ÓA1CŁŹÓëËŤÇúĎßE˝ťÓÚľăFŁŹĘǡń´ćÔÚĘľĘý![]() ŁŹĘš
ŁŹĘš![]() şăłÉÁ˘ŁżČô´ćÔÚŁŹĘÔÇółö
şăłÉÁ˘ŁżČô´ćÔÚŁŹĘÔÇółö![]() ľÄÖľŁťČô˛ť´ćÔÚŁŹÇëËľĂ÷ŔíÓÉ.
ľÄÖľŁťČô˛ť´ćÔÚŁŹÇëËľĂ÷ŔíÓÉ.
˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁş¸ßÖĐĘýѧ Ŕ´Ô´Łş2009Äę¸ßżźĘýѧњÖáĘԞퟯ˝őŁ¨10ŁŠŁ¨˝âÎö°ćŁŠ ĚâĐÍŁş˝â´đĚâ
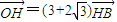 ŁŽĆäÖĐA1ŁŹA2ŁŹBĘÇÔ˛OÓë×řąęÖáľÄ˝ťľăŁŹcÎŞËŤÇúĎ߾İ뽚žŕŁŽ
ŁŽĆäÖĐA1ŁŹA2ŁŹBĘÇÔ˛OÓë×řąęÖáľÄ˝ťľăŁŹcÎŞËŤÇúĎ߾İ뽚žŕŁŽ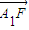 =ŚË
=ŚË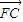 şăłÉÁ˘ŁŹČô´ćÔÚŁŹĘÔÇółöŚËľÄÖľŁťČô˛ť´ćÔÚŁŹÇëËľĂ÷ŔíÓÉŁŽ
şăłÉÁ˘ŁŹČô´ćÔÚŁŹĘÔÇółöŚËľÄÖľŁťČô˛ť´ćÔÚŁŹÇëËľĂ÷ŔíÓÉŁŽ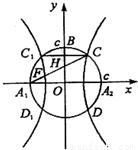
˛éż´´đ°¸şÍ˝âÎö>>
°ŮśČÖÂĐĹ - ÁˇĎ°˛áÁĐąí - ĘÔĚâÁĐąí
şţąąĘĄťĽÁŞÍřÎĽˇ¨şÍ˛ťÁźĐĹϢžŮą¨Ć˝Ě¨ | ÍřÉĎÓĐşŚĐĹϢžŮą¨×¨Çř | ľçĐĹՊƞٹ¨×¨Çř | ÉćŔúʡĐéÎŢÖ÷ŇĺÓĐşŚĐĹϢžŮą¨×¨Çř | ÉćĆóÇÖȨžŮą¨×¨Çř
ÎĽˇ¨şÍ˛ťÁźĐĹϢžŮą¨ľçť°Łş027-86699610 žŮą¨ÓĘĎ䣺58377363@163.com