
【题目】已知椭圆![]() :
: ![]() (
(![]() )的焦距为
)的焦距为![]() ,且经过点
,且经过点![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)![]() 、
、![]() 是椭圆
是椭圆![]() 上两点,线段
上两点,线段![]() 的垂直平分线
的垂直平分线![]() 经过
经过![]() ,求
,求![]() 面积的最大值(
面积的最大值(![]() 为坐标原点).
为坐标原点).
【答案】(Ⅰ) ![]() ;(Ⅱ)
;(Ⅱ) ![]() .
.
【解析】【试题分析】(Ⅰ)由题设条件先求出左、右焦点坐标![]() ,
, ![]() ,再借助椭圆定义求得
,再借助椭圆定义求得![]() ,进而求得椭圆方程;(Ⅱ)先建立直线
,进而求得椭圆方程;(Ⅱ)先建立直线![]() 的方程为
的方程为![]() ,借助坐标之间的关系计算
,借助坐标之间的关系计算![]() ,
, ![]() 到直线
到直线![]() 的距离
的距离![]() ,
, ![]() 的面积函数
的面积函数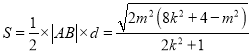 ,最后借助
,最后借助![]() ,从而求得
,从而求得![]() :若
:若![]() ,则
,则![]() ,等号当且仅当
,等号当且仅当![]() 时成立;若
时成立;若![]() ,则
,则![]() ,
, ![]() ,等号当且仅当
,等号当且仅当![]() ,
, ![]() 时成立,最后求得
时成立,最后求得![]() 面积的最大值为
面积的最大值为![]() :
:
解析:(Ⅰ)依题意, ![]() ,椭圆
,椭圆![]() 的焦点为
的焦点为![]() ,
, ![]()
![]()
所以![]() ,椭圆
,椭圆![]() 的方程为
的方程为![]()
(Ⅱ)根据椭圆的对称性,直线![]() 与
与![]() 轴不垂直,设直线
轴不垂直,设直线![]() :
: ![]()
由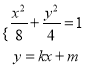 得,
得, ![]()
设![]() ,
, ![]() ,则
,则![]() ,
, ![]()
![]() ,
, ![]() 到直线
到直线![]() 的距离
的距离![]() ,
, ![]() 的面积
的面积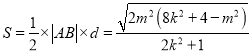
依题意, ![]() ,
, ![]() ,
,
![]()
![]() ,
, ![]() ,代入整理得,
,代入整理得, ![]()
若![]() ,则
,则![]() ,等号当且仅当
,等号当且仅当![]() 时成立
时成立
若![]() ,则
,则![]() ,
, ![]() ,等号当且仅当
,等号当且仅当![]() ,
, ![]() 时成立。
时成立。
综上所述, ![]() 面积的最大值为
面积的最大值为![]()


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
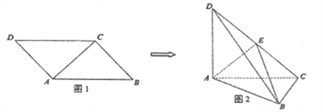
【题目】图1,平行四边形![]() 中,
中, ![]() ,
, ![]() ,现将
,现将![]() 沿
沿![]() 折起,得到三棱锥
折起,得到三棱锥![]() (如图2),且
(如图2),且![]() ,点
,点![]() 为侧棱
为侧棱![]() 的中点.
的中点.
(1)求证: ![]() 平面
平面![]() ;
;
(2)求三棱锥![]() 的体积;
的体积;
(3)在![]() 的角平分线上是否存在点
的角平分线上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,圆锥的轴截面为等腰直角△SAB,Q为底面圆周上一点.

(1)若QB的中点为C,OH⊥SC,求证:OH⊥平面SBQ;
(2)如果∠AOQ=60°,QB=2![]() ,求此圆锥的体积.
,求此圆锥的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校要用甲、乙、丙三辆校车把教职工从老校区接到校本部,已知从老校区到校本部有两条公路,校车走公路①时堵车的概率为![]() ,校车走公路②时堵车的概率为p.若甲、乙两辆校车走公路①,丙校车由于其他原因走公路②,且三辆校车是否堵车相互之间没有影响.
,校车走公路②时堵车的概率为p.若甲、乙两辆校车走公路①,丙校车由于其他原因走公路②,且三辆校车是否堵车相互之间没有影响.
(1)若三辆校车中恰有一辆校车被堵的概率为![]() ,求走公路②堵车的概率;
,求走公路②堵车的概率;
(2)在(1)的条件下,求三辆校车中被堵车辆的辆数ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是抛物线
是抛物线![]() 与圆
与圆![]() 在第一象限的公共点,其中圆心
在第一象限的公共点,其中圆心![]() ,点
,点![]() 到
到![]() 的焦点
的焦点![]() 的距离与
的距离与![]() 的半径相等,
的半径相等, ![]() 上一动点到其准线与到点
上一动点到其准线与到点![]() 的距离之和的最小值等于
的距离之和的最小值等于![]() 的直径,
的直径, ![]() 为坐标原点,则直线
为坐标原点,则直线![]() 被圆
被圆![]() 所截得的弦长为( )
所截得的弦长为( )
A. 2 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com