
【题目】已知函数f(x)=2lnx+1.
(1)若f(x)≤2x+c,求c的取值范围;
(2)设a>0时,讨论函数g(x)=![]() 的单调性.
的单调性.
科目:高中数学 来源: 题型:
【题目】随着资本市场的强势进入,互联网共享单车“忽如一夜春风来”,遍布了各级城市的大街小巷,为了解我市的市民对共享单车的满意度,某调查机构借助网络进行了问卷调查,并从参与调查的网友中随机抽取了50人进行分析.若得分低于60分,说明不满意,若得分不低于60分,说明满意,调查满意度得分情况结果用茎叶图表示如图1.
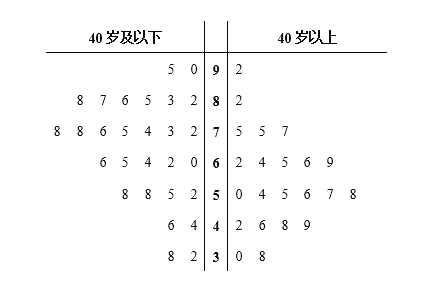
(Ⅰ)根据茎叶图找出40岁以上网友中满意度得分的众数和中位数;
(Ⅱ)根据茎叶图完成下面列联表,并根据以上数据,判断是否有![]() 的把握认为满意度与年龄有关;
的把握认为满意度与年龄有关;
满意 | 不满意 | 合计 | |
40岁以下 | |||
40岁以上 | |||
合计 |
(Ⅲ)先采用分层抽样的方法从40岁及以下的网友中选取7人,再从这7人中随机选出2人,将频率视为概率,求选出的2人中至少有1人是不满意的概率.
参考格式: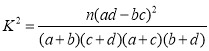 ,其中
,其中![]()
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 为圆锥的顶点,
为圆锥的顶点,![]() 是圆锥底面的圆心,
是圆锥底面的圆心,![]() 是底面的内接正三角形,
是底面的内接正三角形,![]() 为
为![]() 上一点,∠APC=90°.
上一点,∠APC=90°.
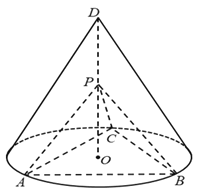
(1)证明:平面PAB⊥平面PAC;
(2)设DO=![]() ,圆锥的侧面积为
,圆锥的侧面积为![]() ,求三棱锥PABC的体积.
,求三棱锥PABC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为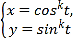
![]() 为参数
为参数![]() .以坐标原点为极点,
.以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)当![]() 时,
时,![]() 是什么曲线?
是什么曲线?
(2)当![]() 时,求
时,求![]() 与
与![]() 的公共点的直角坐标.
的公共点的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知三棱柱ABC-A1B1C1的底面是正三角形,侧面BB1C1C是矩形,M,N分别为BC,B1C1的中点,P为AM上一点,过B1C1和P的平面交AB于E,交AC于F.
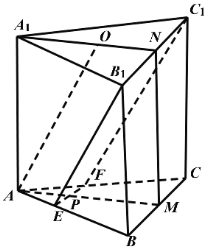
(1)证明:AA1∥MN,且平面A1AMN⊥EB1C1F;
(2)设O为△A1B1C1的中心,若AO∥平面EB1C1F,且AO=AB,求直线B1E与平面A1AMN所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为实现国民经济新“三步走”的发展战略目标,国家加大了扶贫攻坚的力度.某地区在2015 年以前的年均脱贫率(脱离贫困的户数占当年贫困户总数的比)为![]() .2015年开始,全面实施“精准扶贫”政策后,扶贫效果明显提高,其中2019年度实施的扶贫项目,各项目参加户数占比(参加该项目户数占 2019 年贫困户总数的比)及该项目的脱贫率见下表:
.2015年开始,全面实施“精准扶贫”政策后,扶贫效果明显提高,其中2019年度实施的扶贫项目,各项目参加户数占比(参加该项目户数占 2019 年贫困户总数的比)及该项目的脱贫率见下表:
实施项目 | 种植业 | 养殖业 | 工厂就业 | 服务业 |
参加用户比 |
|
|
|
|
脱贫率 |
|
|
|
|
那么![]() 年的年脱贫率是实施“精准扶贫”政策前的年均脱贫率的( )
年的年脱贫率是实施“精准扶贫”政策前的年均脱贫率的( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学生兴趣小组随机调查了某市100天中每天的空气质量等级和当天到某公园锻炼的人次,整理数据得到下表(单位:天):
锻炼人次 空气质量等级 | [0,200] | (200,400] | (400,600] |
1(优) | 2 | 16 | 25 |
2(良) | 5 | 10 | 12 |
3(轻度污染) | 6 | 7 | 8 |
4(中度污染) | 7 | 2 | 0 |
(1)分别估计该市一天的空气质量等级为1,2,3,4的概率;
(2)求一天中到该公园锻炼的平均人次的估计值(同一组中的数据用该组区间的中点值为代表);
(3)若某天的空气质量等级为1或2,则称这天“空气质量好”;若某天的空气质量等级为3或4,则称这天“空气质量不好”.根据所给数据,完成下面的2×2列联表,并根据列联表,判断是否有95%的把握认为一天中到该公园锻炼的人次与该市当天的空气质量有关?
人次≤400 | 人次>400 | |
空气质量好 | ||
空气质量不好 |
附: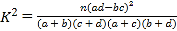 ,
,
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com