练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，在多面体ABCDE中，平面平面ABC，，，，且，.

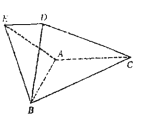
    （1）求AB的长；

    （2）若，求多面体ABCDE的体积.

    【答案】（1）；（2）.

    【解析】

    （1）根据面面垂直的性质定理，结合线面垂直的判定定理、平行线的性质，可以证明出，最后利用勾股定理求解即可.

    （2）利用四棱锥的体积公式进行求解即可.

    （1）连接，因为平面平面ABC，平面平面ABC=AB，，因此有平面，而平面，所以,又因为，

    所以，又因为，而平面,因此有

    平面，平面，所以有，因为，所以

    ；

    （2）因为，且，所以四边形是梯形，故多面体ABCDE是四棱锥.由（1）可知：平面，因此四棱锥的高为，

    ，而，由（1）可知：平面，而平面，所以，所以梯形的面积为：，

    四棱锥的体积为：，因此多面体ABCDE的体积为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）讨论的单调性；

    （2）若在区间上有两个零点，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知直线的参数方程为（， 为参数），曲线的极坐标方程为.

    (1)将曲线的极坐标方程化为直角坐标方程，并说明曲线的形状；

    (2)若直线经过点，求直线被曲线截得的线段的长.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在①；②，这两个条件中任选一个，补充在下面问题中，然后解答补充完整的题目.

    在中，内角的对边分别为，设的面积为，已知 .

    （1）求的值；

    （2）若，求的值.

    注：如果选择多个条件分别解答，按第一个解答计分.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

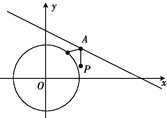
    【题目】唐代诗人李颀的诗《古从军行》开头两句说:“白日登山望烽火,黄昏饮马傍交河.”诗中隐含着一个有趣的数学问题——“将军饮马”,即将军在观望烽火之后从山脚下某处出发,先到河边饮马再回到军营,怎样走才能使总路程最短?在如图所示的直角坐标系xOy中,设军营所在平面区域为{(x,y)|x2+y2≤},河岸线所在直线方程为x+2y-4=0.假定将军从点P(,)处出发,只要到达军营所在区域即回到军营,当将军选择最短路程时,饮马点A的纵坐标为______.最短总路程为______

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在口中， ，沿将翻折到的位置，使平面平面.

    （1）求证： 平面；

    （2）若在线段上有一点满足，且二面角的大小为，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知定圆，动圆过点且与圆相切，记动圆圆心的轨迹为.

    （1）求轨迹的方程

    （2）若轨迹上存在两个不同点，关于直线对称，求面积的最大值（为坐标原点）.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱台中，底面是正方形，且，点，分别为棱，的中点，二面角的平面角大小为.

    （1）证明：；

    （2）求直线与平面所成角的正弦值.

    查看答案和解析>>

    同步练习册答案