
【题目】甲乙两支围棋队各5名队员按事先排好的顺序进行擂台赛,双方1号队员先赛,负者被淘汰;然后负方的2号队员再与对方的胜者比赛,负者又被淘汰.依次类推,直到有一方队员全部被淘汰,则宣布另一方获胜.假设每名队员的实力相当,则比赛结束时甲队未上场队员数![]() 的数学期望
的数学期望![]() ______.
______.
科目:高中数学 来源: 题型:
【题目】某地政府为科技兴市,欲将如图所示的一块不规则的非农业用地![]() 规划建成一个矩形的高科技工业园区.已知
规划建成一个矩形的高科技工业园区.已知![]() ,
,![]() ,
,![]() ,曲线段
,曲线段![]() 是以点
是以点![]() 为顶点且开口向上的抛物线的一段.如果要使矩形的相邻两边分别落在
为顶点且开口向上的抛物线的一段.如果要使矩形的相邻两边分别落在![]() 、
、![]() 上,且一个顶点
上,且一个顶点![]() 落在曲线段
落在曲线段![]() 上,问应如何规划才能使矩形工业园区的用地面积最大?并求出最大的用地面积(精确到
上,问应如何规划才能使矩形工业园区的用地面积最大?并求出最大的用地面积(精确到![]() ).
).

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
,![]()
(1)当![]() 时,求
时,求![]() 的单调区间;
的单调区间;
(2)①证明:当![]() 时,函数
时,函数![]() 在
在![]() 上恰有一个极值点
上恰有一个极值点![]() ;
;
②求实数![]() 的取值范围,使得对任意的
的取值范围,使得对任意的![]() ,恒有
,恒有![]() 成立.
成立.
注:![]() 为自然对数的底数.
为自然对数的底数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某大型活动中,甲、乙等五名志愿者被随机地分到A,B,C,D四个不同的岗位服务,每个岗位至少有一名志愿者.
(1)求甲、乙两人同时参加A岗位服务的概率;
(2)求甲、乙两人不在同一个岗位服务的概率;
(3)求五名志愿者中仅有一人参加A岗位服务的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了进一步激发同学们的学习热情,某班级建立了数学英语两个学习兴趣小组,两组的人数如下表所示:
组别 性别 | 数学 | 英语 |
男 | 5 | 1 |
女 | 3 | 3 |
现采用分层抽样的方法(层内采用简单随机抽样)从两组中共抽取3名同学进行测试.
(1)求从数学组抽取的同学中至少有1名女同学的概率;
(2)记ξ为抽取的3名同学中男同学的人数,求随机变量ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,四棱锥![]() 中,侧面
中,侧面![]() 底面
底面![]() ,底面
,底面![]() 是平行四边形,
是平行四边形,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 中点,点
中点,点![]() 在线段
在线段![]() 上.
上.
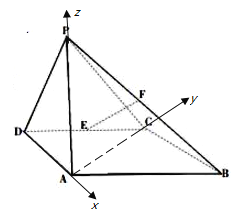
(Ⅰ)证明:![]() ;
;
(Ⅱ)若![]()
![]()
![]()
![]() ,求实数
,求实数![]() 使直线
使直线![]() 与平面
与平面![]() 所成角和直线
所成角和直线![]() 与平面
与平面![]() 所成角相等.
所成角相等.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出以下四个说法,其中正确的说法是( )
A.残差点分布的带状区域的宽度越窄相关指数越小;
B.在刻画回归模型的拟合效果时,相关指数![]() 的值越大,说明拟合的效果越好;
的值越大,说明拟合的效果越好;
C.在回归直线方程![]() 中,当解释变量
中,当解释变量![]() 每增加一个单位时,预报变量
每增加一个单位时,预报变量![]() 平均增加0.2个单位;
平均增加0.2个单位;
D.对分类变量![]() 与
与![]() ,若它们的随机变量
,若它们的随机变量![]() 的观测值
的观测值![]() 越小,则判断“
越小,则判断“![]() 与
与![]() 有关系”的把握程度越大.
有关系”的把握程度越大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com