【答案】
分析:(1)讨论含参数的函数的单调性问题,先求出导函数f′(x),令f′(x)>0,本小题要对参数a分a≥0,-1<a<0,a≤-1三种情形进行讨论,对运算能力要求较高;
(2),由(1)的结论-1<a=
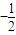
<0,所以分三个单调区间来利用单调性来讨论函数的零点的个数问题.
(3)是近年来高考考查的热点问题,即与函数结合证明不等式问题,常用的解题思路是利用前面的结论构造函数,利用函数的单调性,对于函数取单调区间上的正整数自变量n有某些结论成立,进而解答出这类不等式问题的解.
解答:解:(1)
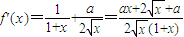
,
若a≥0,则f′(x)>0,f(x)在定义域内单调递增;若a≤-1,
则f′(x)<0,f(x)在定义域内单调递减;若-1<a<0,由f′(x)=0
解得,
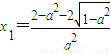
,
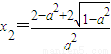
,
直接讨论f′(x)知,f(x)在
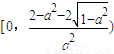
和
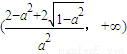
单调递减,
在
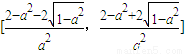
单调递增.
(2)观察得f(0)=0,
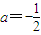
时,
由①得f(x)在
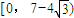
单调递减,
所以f(x)在
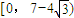
上有且只有一个零点;
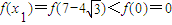
,
计算得
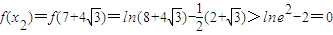
,
f(x
1)f(x
2)<0且f(x)在区间
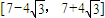
单调递增,
所以f(x)在
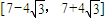
上有且只有一个零点;
根据对数函数与幂函数单调性比较知,
存在充分大的M∈R,使f(M)<0,f(x
2)f(M)<0
且f(x)在区
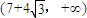
单调递减,
所以f(x)在
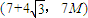
上
从而在
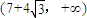
上有且只有一个零点.
综上所述,
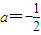
时,f(x)有3个零点.
(3)取a=-1,
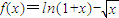
,
由①得f(x)单调递减,
所以?x>0,f(x)<f(0)=0,
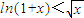
,
从而ln(1+
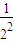
)(1+
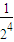
)…(1+
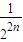
)
=ln(1+
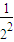
)ln(1+
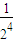
)+…(1+
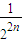
)
<

+

+…
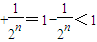
,
由lnx单调递增得
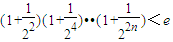
.
点评:单调性刻画函数两个变量变化趋势的一致性,是认识函数的重要角度,运用单调性可以确定函数零点的个数,考查导数使单调性可以定量、精确研究这一重要工具.参数是可变的常数,处理参数是比较高端的数学素养,本题考查了这一素养,因此对学生的综合应用能力要求较高.

 ,a∈R是常数.
,a∈R是常数.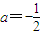 时,f(x)零点的个数;
时,f(x)零点的个数;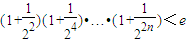 (n∈N*,e为自然对数的底数).
(n∈N*,e为自然对数的底数).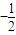 <0,所以分三个单调区间来利用单调性来讨论函数的零点的个数问题.
<0,所以分三个单调区间来利用单调性来讨论函数的零点的个数问题.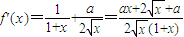 ,
,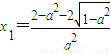 ,
,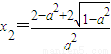 ,
,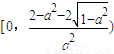
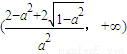 单调递减,
单调递减,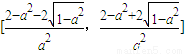 单调递增.
单调递增.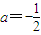 时,
时,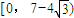 单调递减,
单调递减,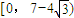 上有且只有一个零点;
上有且只有一个零点;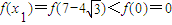 ,
,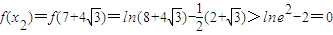 ,
,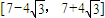 单调递增,
单调递增,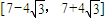 上有且只有一个零点;
上有且只有一个零点;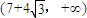 单调递减,
单调递减,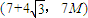 上
上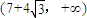 上有且只有一个零点.
上有且只有一个零点.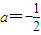 时,f(x)有3个零点.
时,f(x)有3个零点.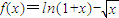 ,
,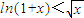 ,
,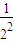 )(1+
)(1+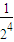 )…(1+
)…(1+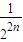 )
)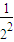 )ln(1+
)ln(1+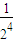 )+…(1+
)+…(1+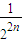 )
) +
+ +…
+…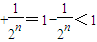 ,
,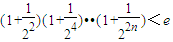 .
.

 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案