
【题目】某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为[40,50],[50,60],…,[80,90],[90,100] 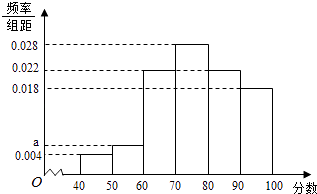
(1)求频率分布图中a的值;
(2)估计该企业的职工对该部门评分不低于80的概率;
(3)从评分在[40,60]的受访职工中,随机抽取2人,求此2人评分都在[40,50]的概率.
【答案】
(1)解:因为(0.004+a+0.018+0.022×2+0.028)×10=1,解得a=0.006
(2)解:由已知的频率分布直方图可知,50名受访职工评分不低于80的频率为(0.022+0.018)×10=0.4,所以该企业职工对该部门评分不低于80的概率的估计值为0.4;
(3)解:受访职工中评分在[50,60)的有:50×0.006×10=3(人),记为A1,A2,A3;
受访职工评分在[40,50)的有:50×0.004×10=2(人),记为B1,B2.
从这5名受访职工中随机抽取2人,所有可能的结果共有10种,
分别是{A1,A2},{A1,A3},{A1,B1},{A1,B2},{A2,A3},{A2,B1},{A2,B2},{A3,B1},{A3,B2},{B1,B2},
又因为所抽取2人的评分都在[40,50)的结果有1种,即{B1,B2},
故所求的概率为P= ![]()
【解析】(1)利用频率分布直方图中的信息,所有矩形的面积和为1,得到a;(2)对该部门评分不低于80的即为90和100,的求出频率,估计概率;(3)求出评分在[40,60]的受访职工和评分都在[40,50]的人数,随机抽取2人,列举法求出所有可能,利用古典概型公式解答.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:高中数学 来源: 题型:
【题目】已知等比数列{an}的各项均为正数,且a1a100+a3a98=8,则log2a1+log2a2+…+log2a100=( )
A.10
B.50
C.100
D.1000
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,其离心率
,其离心率![]() ,以原点为圆心,椭圆的半焦距为半径的圆与直线
,以原点为圆心,椭圆的半焦距为半径的圆与直线![]() 相切.
相切.
(1)求![]() 的方程;
的方程;
(2)过![]() 的直线
的直线![]() 交
交![]() 于
于![]() 两点,
两点, ![]() 为
为![]() 的中点,连接
的中点,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,若四边形
,若四边形![]() 的面积
的面积![]() 满足:
满足: ![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A. 简单随机抽样每个个体被抽到的机会不一样,与先后有关
B. 由生物学知道生男生女的概率均为![]() ,一对夫妇生两个孩子,则一定为一男一女
,一对夫妇生两个孩子,则一定为一男一女
C. 互斥事件一定是对立事件,对立事件不一定是互斥事件
D. 老师在某班学号为1~50的50名学生中依次抽取学号为5,10,15,20,25,30,35,40,45,50的学生进行作业检查,这种抽样方法是系统抽样
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:
①在△ABC中,若A<B,则sinA<sinB;
②在同一坐标系中,函数y=sinx与y=lgx的交点个数为2个;
③函数y=|tan2x|的最小正周期为 ![]() ;
;
④存在实数x,使2sin(2x﹣ ![]() )﹣1=
)﹣1= ![]() 成立;
成立;
其中正确的命题为(写出所有正确命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区拟建立一个艺术博物馆,采取竞标的方式从多家建筑公司选取一家建筑公司,经过层层筛选,甲、乙两家建筑公司进入最后的招标.现从建筑设计院聘请专家设计了一个招标方案:两家公司从![]() 个招标问题中随机抽取
个招标问题中随机抽取![]() 个问题,已知这
个问题,已知这![]() 个招标问题中,甲公司可正确回答其中的
个招标问题中,甲公司可正确回答其中的![]() 道題目,而乙公司能正确回答毎道题目的概率均为
道題目,而乙公司能正确回答毎道题目的概率均为![]() ,甲、乙两家公司对每题的回答都是相互独立,互不影响的.
,甲、乙两家公司对每题的回答都是相互独立,互不影响的.
(1)求甲、乙两家公司共答对![]() 道题目的概率;
道题目的概率;
(2)请从期望和方差的角度分析,甲、乙两家哪家公司竞标成功的可能性更大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知P为△ABC内一点,且满足 ![]() ,记△ABP,△BCP,△ACP的面积依次为S1 , S2 , S3 , 则S1:S2:S3等于( )
,记△ABP,△BCP,△ACP的面积依次为S1 , S2 , S3 , 则S1:S2:S3等于( )
A.1:2:3
B.1:4:9
C.2:3:1
D.3:1:2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱![]() 中,各棱长均为6,
中,各棱长均为6, ![]() 分别是侧棱
分别是侧棱![]() 、
、![]() 上的点,且
上的点,且![]() .
.
(1)在![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ?证明你的结论;
?证明你的结论;
(2)求异面直线![]() 与
与![]() 所成角的余弦值.
所成角的余弦值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com