
 ��
�� ���������ɺ���h��x��������a��0��b��0����h��x����b��a��[1��2]���������ʵ��b��ȡֵ��Χ��
���������ɺ���h��x��������a��0��b��0����h��x����b��a��[1��2]���������ʵ��b��ȡֵ��Χ��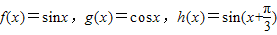 ���úͽǹ�ʽ���ɵõ�
���úͽǹ�ʽ���ɵõ�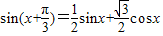 ����h��x��Ϊf��x����g��x�����������ɺ�����
����h��x��Ϊf��x����g��x�����������ɺ�����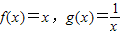 �����������ɺ���h��x��������a��0��b��0���ɵ�h��x��=ax+
�����������ɺ���h��x��������a��0��b��0���ɵ�h��x��=ax+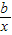 ���ٽ�Ϻ���h��x�����������ú��������Ľⷨ�������ʵ��b��ȡֵ��Χ��
���ٽ�Ϻ���h��x�����������ú��������Ľⷨ�������ʵ��b��ȡֵ��Χ�� ��
��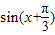 =asinx+bcosx��
=asinx+bcosx�� ����ʽ������
����ʽ������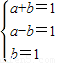 ���Dz����ܳ����ģ�
���Dz����ܳ����ģ�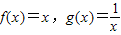 �����������ɺ���h��x��������a��0��b��0��
�����������ɺ���h��x��������a��0��b��0��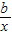 ��
��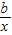 ��b��a��[1��2]�������
��b��a��[1��2]�������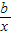 ����Сֵ���ɣ�
����Сֵ���ɣ�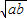 ����
����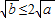 ��
��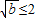 ����0��b��4
����0��b��4

 ֥�鿪���γ�������ϵ�д�
֥�鿪���γ�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 1 |
| 4 |
| x |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| x |
| 1 |
| x |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| �� |
| 3 |
| 1 |
| x |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| ||
| 2 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com