
【题目】椭圆 ![]() 的左右焦点分别为F1 , F2 , 离心率为
的左右焦点分别为F1 , F2 , 离心率为 ![]() ,过点F1且垂直于x轴的直线被椭圆截得的弦长为
,过点F1且垂直于x轴的直线被椭圆截得的弦长为 ![]() ,直线l:y=kx+m与椭圆交于不同的A,B两点.
,直线l:y=kx+m与椭圆交于不同的A,B两点.
(1)求椭圆C的方程;
(2)若在椭圆C上存在点Q满足: ![]() (O为坐标原点).求实数λ的取值范围.
(O为坐标原点).求实数λ的取值范围.
【答案】
(1)解:由已知得 ![]() ,
, ![]() ,又a2=b2+c2,联立解得
,又a2=b2+c2,联立解得 ![]() .
.
故所求椭圆C的方程为 ![]() .
.
(2)解:设A(x1,y1),B(x2,y2),Q(x0,y0)
当λ=0时由 ![]() 知,
知, ![]() ,A与B关于原点对称,存在Q满足题意,∴λ=0成立.
,A与B关于原点对称,存在Q满足题意,∴λ=0成立.
当λ≠0时,设直线AB的方程为y=kx+m.
联立 ![]() 得(1+2k2)x2+4kmx+2m2﹣2=0,
得(1+2k2)x2+4kmx+2m2﹣2=0,
由△=(4km)2﹣4(1+2k2)(2m2﹣2)>0解得m2<1+2k2…(*)
∴ ![]() ,
, ![]() .
.
由 ![]() ,得(x1+x2,y1+y2)=(λx0,λy0),可得x1+x2=λx0,y1+y2=λy0,
,得(x1+x2,y1+y2)=(λx0,λy0),可得x1+x2=λx0,y1+y2=λy0,
∴  ,
,
代入到 ![]() 得到
得到 ![]() ,
,
代入(*)式 ![]() ,
,
由1+2k2>0得λ2<4,解得﹣2<λ<2且λ≠0.
∴综上λ∈(﹣2,2).
【解析】(1)由已知得 ![]() ,
, ![]() ,又a2=b2+c2 , 联立解得即可.(2)设A(x1 , y1),B(x2 , y2),Q(x0 , y0),分类讨论:当λ=0时,利用椭圆的对称性即可得出;λ≠0时,设直线AB的方程为y=kx+m.与椭圆的方程联立得到△>0及根与系数的关系,再利用向量相等,代入计算即可得出.
,又a2=b2+c2 , 联立解得即可.(2)设A(x1 , y1),B(x2 , y2),Q(x0 , y0),分类讨论:当λ=0时,利用椭圆的对称性即可得出;λ≠0时,设直线AB的方程为y=kx+m.与椭圆的方程联立得到△>0及根与系数的关系,再利用向量相等,代入计算即可得出.
【考点精析】解答此题的关键在于理解椭圆的标准方程的相关知识,掌握椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,底面ABCD为直角梯形,AD∥BC,∠BAD=90°,PA=AD=AB=2BC=2,过AD的平面分别交PB,PC于M,N两点. 
(1)求证:MN∥BC;
(2)若M,N分别为PB,PC的中点,
①求证:PB⊥DN;
②求二面角P﹣DN﹣A的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆O:x2+y2=2,直线l:y=kx﹣2.
(1)若直线l与圆O交于不同的两点A,B,当 ![]() 时,求k的值;
时,求k的值;
(2)若 ![]() 是直线l上的动点,过P作圆O的两条切线PC、PD,切点为C、D,探究:直线CD是否过定点?若过定点则求出该定点,若不存在则说明理由;
是直线l上的动点,过P作圆O的两条切线PC、PD,切点为C、D,探究:直线CD是否过定点?若过定点则求出该定点,若不存在则说明理由;
(3)若EF、GH为圆O:x2+y2=2的两条相互垂直的弦,垂足为 ![]() ,求四边形EGFH的面积的最大值.
,求四边形EGFH的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2014年“五一节”期间,高速公路车辆较多,交警部门通过路面监控装置抽样调查某一山区路段汽车行驶速度,采用的方法是:按到达监控点先后顺序,每隔50辆抽取一辆,总共抽取120辆,分别记下其行车速度,将行车速度(km/h)分成七段[60,65),[65,70),[70,75),[75,80),[80,85),[85,90),[90,95)后得到如图所示的频率分布直方图,据图解答下列问题: 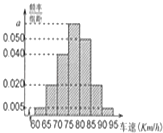
(1)求a的值,并说明交警部门采用的是什么抽样方法?
(2)求这120辆车行驶速度的众数和中位数的估计值(精确到0.1);
(3)若该路段的车速达到或超过90km/h即视为超速行驶,试根据样本估计该路段车辆超速行驶的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下命题:
①若x≠1或y≠2,则x+y≠3;
②若空间向量 ![]() ,
, ![]() 与空间中任一向量都不能组成空间的一组基底,则
与空间中任一向量都不能组成空间的一组基底,则 ![]() 与
与 ![]() 共线;
共线;
③命题“x∈R,使得x2+x+1<0”的否定是:“x∈R,均有x2+x+1<0”;
④若A、B为两个定点,K为正常数,若|PA|+|PB|=K,则动点P的轨迹是椭圆;
⑤已知抛物线y2=2px,以过焦点的一条弦AB为直径作圆,则此圆与准线相切.
其中真命题有( )个.
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位用2160万元购得一块空地,计划在该地块上建造一栋至少10层,每层2000平方米的楼房.经测算,如果将楼房建为x(x≥10)层,则每平方米的平均建筑费用为560+48x(单位:元).
(注:平均综合费用=平均建筑费用+平均购地费用,平均购地费用= ![]() )
)
(1)写出楼房平均综合费用y关于建造层数x的函数关系式;
(2)该楼房应建造多少层时,可使楼房每平方米的平均综合费用最少?最少值是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】点P是双曲线 ![]() ﹣y2=1的右支上一点,M、N分别是(x+
﹣y2=1的右支上一点,M、N分别是(x+ ![]() )2+y2=1和(x﹣
)2+y2=1和(x﹣ ![]() )2+y2=1上的点,则|PM|﹣|PN|的最大值是( )
)2+y2=1上的点,则|PM|﹣|PN|的最大值是( )
A.2
B.4
C.6
D.8
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥S﹣ABCD的底面ABCD是正方形,SA⊥底面ABCD,E是SC上的任意一点.过点E的平面α垂直于平面SAC. 
(1)请作出平面α截四棱锥S﹣ABCD的截面(只需作图并写出作法);
(2)当SA=AB时,求二面角B﹣SC﹣D的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com