
【题目】在平面直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴建立极坐标系.已知曲线
轴正半轴为极轴建立极坐标系.已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,射线
,射线![]() 与曲线
与曲线![]() 交于点
交于点![]() ,点
,点![]() 满足
满足![]() ,设倾斜角为
,设倾斜角为![]() 的直线
的直线![]() 经过点
经过点![]() .
.
(1)求曲线![]() 的直角坐标方程及直线
的直角坐标方程及直线![]() 的参数方程;
的参数方程;
(2)直线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点,当
两点,当![]() 为何值时,
为何值时,![]() 最大?求出此最大值.
最大?求出此最大值.
科目:高中数学 来源: 题型:
【题目】已知函数 下列关于函数
下列关于函数![]() 的零点个数判断正确的是( )
的零点个数判断正确的是( )
A.当![]() 时,至少有2个零点B.当
时,至少有2个零点B.当![]() 时,至多有9个零点
时,至多有9个零点
C.当![]() 时,至少有4个零点D.当
时,至少有4个零点D.当![]() 时,至多有4个零点
时,至多有4个零点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 、
、![]() 、
、![]() 是集合,称
是集合,称![]() 为有序三元组,如果集合
为有序三元组,如果集合![]() 、
、![]() 、
、![]() 满足
满足![]()
![]() ,且
,且![]() ,则称有序三元组
,则称有序三元组![]() 为最小相交(其中
为最小相交(其中![]() 表示集合
表示集合![]() 中的元素个数),如集合
中的元素个数),如集合![]() ,
,![]() ,
,![]() 就是最小相交有序三元组,则由集合
就是最小相交有序三元组,则由集合![]() 的子集构成的最小相交有序三元组的个数是________
的子集构成的最小相交有序三元组的个数是________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了响应国家号召,某校组织部分学生参与了“垃圾分类,从我做起”的知识问卷作答,并将学生的作答结果分为“合格”与“不合格”两类与“问卷的结果”有关?
不合格 | 合格 | |
男生 | 14 | 16 |
女生 | 10 | 20 |
(1)是否有90%以上的把握认为“性别”与“问卷的结果”有关?
(2)在成绩合格的学生中,利用性别进行分层抽样,共选取9人进行座谈,再从这9人中随机抽取5人发送奖品,记拿到奖品的男生人数为X,求X的分布列及数学期望![]() .
.
附: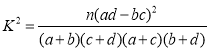
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.703 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义![]() ,已知函数
,已知函数![]() 、
、![]() 定义域都是
定义域都是![]() ,给出下列命题:
,给出下列命题:
(1)若![]() 、
、![]() 都是奇函数,则函数
都是奇函数,则函数![]() 为奇函数;
为奇函数;
(2)若![]() 、
、![]() 都是减函数,则函数
都是减函数,则函数![]() 为减函数;
为减函数;
(3)若![]() ,
,![]() ,则
,则![]() ;
;
(4)若![]() 、
、![]() 都是周期函数,则函数
都是周期函数,则函数![]() 是周期函数.
是周期函数.
其中正确命题的个数为( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() (
(![]() 为常数).
为常数).
(i)给出下列结论:
①曲线![]() 为中心对称图形;
为中心对称图形;
②曲线![]() 为轴对称图形;
为轴对称图形;
③当![]() 时,若点
时,若点![]() 在曲线
在曲线![]() 上,则
上,则![]() 或
或![]() .
.
其中,所有正确结论的序号是_________.
(ii)当![]() 时,若曲线
时,若曲线![]() 所围成的区域的面积小于
所围成的区域的面积小于![]() ,则
,则![]() 的值可以是_________.(写出一个即可)
的值可以是_________.(写出一个即可)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{2n﹣1}的前n项1,3,7,…,2n﹣1组成集合![]() (n∈N*),从集合An中任取k(k=1,2,3,…,n)个数,其所有可能的k个数的乘积的和为Tk(若只取一个数,规定乘积为此数本身),记Sn=T1+T2+…+Tn,例如当n=1时,A1={1},T1=1,S1=1;当n=2时,A2={1,3},T1=1+3,T2=1×3,S2=1+3+1×3=7,试写出Sn=__.
(n∈N*),从集合An中任取k(k=1,2,3,…,n)个数,其所有可能的k个数的乘积的和为Tk(若只取一个数,规定乘积为此数本身),记Sn=T1+T2+…+Tn,例如当n=1时,A1={1},T1=1,S1=1;当n=2时,A2={1,3},T1=1+3,T2=1×3,S2=1+3+1×3=7,试写出Sn=__.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足
满足![]() ,
,![]() ,我们知道当a取不同的值时,得到不同的数列.如当
,我们知道当a取不同的值时,得到不同的数列.如当![]() 时,得到无穷数列:0,
时,得到无穷数列:0,![]() ,
,![]() ,
,![]() ,…,当
,…,当![]() 时,得到有穷数列:
时,得到有穷数列:![]() ,
,![]() ,1.
,1.
(1)当a为何值时,![]() ;
;
(2)设数列![]() 满足
满足![]() ,
,![]() ,求证:a取
,求证:a取![]() 中的任一数,都可以得到一个有穷数列
中的任一数,都可以得到一个有穷数列![]() ;
;
(3)是否存在实数a,使得到的![]() 是无穷数列,且对于任意
是无穷数列,且对于任意![]() ,都有
,都有![]() 成立,若存在,求出a的取值范围;若不存在,请说明理由.
成立,若存在,求出a的取值范围;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com