
【题目】某品牌新款夏装即将上市,为了对新款夏装进行合理定价,在该地区的三家连锁店各进行了两天试销售,得到如下数据:
连锁店 | A店 | B店 | C店 | |||
售价x(元) | 80 | 86 | 82 | 88 | 84 | 90 |
销量y(元) | 88 | 78 | 85 | 75 | 82 | 66 |
(1)分别以三家连锁店的平均售价与平均销量为散点,如A店对应的散点为![]() ,求出售价与销量的回归直线方程
,求出售价与销量的回归直线方程![]() ;
;
(2)在大量投入市场后,销量与单价仍然服从(1)中的关系,且该夏装成本价为40元/件,为使该新夏装在销售上获得最大利润,该款夏装的单价应定为多少元?(保留整数)
附: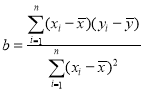 ,
,![]() .
.
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源: 题型:
【题目】如图,在底面是正方形的四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() 是
是![]() 的中点.
的中点.

(1)求证:![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分12分)已知椭圆![]() ,直线
,直线![]() 不过原点
不过原点![]() 且不平行于坐标轴,
且不平行于坐标轴,![]() 与
与![]() 有两个交点
有两个交点![]() ,
,![]() ,线段
,线段![]() 的中点为
的中点为![]() .
.
(Ⅰ)证明:直线![]() 的斜率与
的斜率与![]() 的斜率的乘积为定值;
的斜率的乘积为定值;
(Ⅱ)若![]() 过点
过点![]() ,延长线段
,延长线段![]() 与
与![]() 交于点
交于点![]() ,四边形
,四边形![]() 能否为平行四边形?若能,求此时
能否为平行四边形?若能,求此时![]() 的斜率,若不能,说明理由.
的斜率,若不能,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为培养学生的兴趣爱好,提高学生的综合素养,在高一年级开设各种形式的校本课程供学生选择(如书法讲座、诗歌鉴赏、奥赛讲座等).现统计了某班50名学生一周用在兴趣爱好方面的学习时间(单位:h)的数据,按照[0,2),[2,4),[4,6),[6,8),[8,10]分成五组,得到了如下的频率分布直方图.
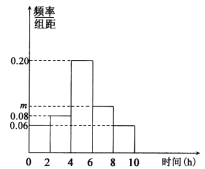
(1)求频率分布直方图中m的值及该班学生一周用在兴趣爱好方面的平均学习时间;
(2)从[4,6),[6,8)两组中按分层抽样的方法抽取6人,再从这6人中抽取2人,求恰有1人在[6,8)组中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 的内角
的内角![]() 、
、![]() 、
、![]() 的对边分别为
的对边分别为![]() 、
、![]() 、
、![]() ,
,![]() 为
为![]() 内一点,若分别满足下列四个条件:
内一点,若分别满足下列四个条件:
①![]() ;
;
②![]() ;
;
③![]() ;
;
④![]() ;
;
则点![]() 分别为
分别为![]() 的( )
的( )
A.外心、内心、垂心、重心B.内心、外心、垂心、重心
C.垂心、内心、重心、外心D.内心、垂心、外心、重心
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例.若输入n,x的值分别为5,2,则输出v的值为( )

A. 64 B. 68
C. 72 D. 133
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥![]() 的底面是边长为
的底面是边长为![]() 的菱形,
的菱形,![]() ,点E是棱BC的中点,
,点E是棱BC的中点,![]() ,点P在平面ABCD的射影为O,F为棱PA上一点.
,点P在平面ABCD的射影为O,F为棱PA上一点.

![]() 1
1![]() 求证:平面
求证:平面![]() 平面BCF;
平面BCF;
![]() 2
2![]() 若
若![]() 平面PDE,
平面PDE,![]() ,求四棱锥
,求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com