
【题目】某校高三有500名学生,在一次考试的英语成绩服从正态分布![]() ,数学成绩的频率分布直方图如下:
,数学成绩的频率分布直方图如下:

(Ⅰ)如果成绩大于135的为特别优秀,则本次考试英语、数学特别优秀的大约各多少人?
(Ⅱ)试问本次考试英语和数学的成绩哪个较高,并说明理由.
(Ⅲ)如果英语和数学两科都特别优秀的共有6人,从(Ⅰ)中的这些同学中随机抽取3人,设三人中两科都特别优秀的有![]() 人,求
人,求![]() 的分布列和数学期望。
的分布列和数学期望。
参考公式及数据:
若![]() ,则
,则![]() ,
,
![]() ,
,![]() .
.
【答案】(1)英语、数学特别优秀的大约各10,12; (2)英语的平均成绩更高; (3)![]()
【解析】
(1)先求出英语和数学特别优秀的的概率,由此能求出英语和数学都特别优秀的人数;
(2)分别计算得到英语和数学的平均分,比较平均分的大小,可得到结论;
(3)由题意得![]() 的所有可能的值为
的所有可能的值为![]() ,分别求出相应的概率,由此得到
,分别求出相应的概率,由此得到![]() 的分布列,求解数学期望.
的分布列,求解数学期望.
(1)![]() 英语成绩服从正态分布
英语成绩服从正态分布![]() ,
,
∴英语成绩特别优秀的概率为![]()
数学成绩特别优秀的概率为![]() ,
,
∴英语成绩特别优秀的同学有![]() 人,
人,
数学成绩特别优秀的同学有![]() 人.
人.
(2)英语的平均成绩为100分,数学的平均成绩为
![]()
因为![]() ,
,
所以英语的平均成绩更高.
(3)英语和数学都特别优秀的有6人,单科优秀的有10人,![]() 可取得值有0,1,2,3,
可取得值有0,1,2,3,
![]() ;
; ![]() ;
;
![]() ;
;![]()
故![]() 的分布列为:
的分布列为:
| 0 | 1 | 2 | 3 |
|
|
|
|
|
![]() 的数学期望为
的数学期望为![]() (人).
(人).
或:因![]() 服从超几何分布,所以
服从超几何分布,所以![]()


科目:高中数学 来源: 题型:
【题目】已知函数![]() 且
且![]() ,函数
,函数![]() 在点
在点![]() 处的切线过点
处的切线过点 ![]() .
.
(1) 求![]() 满足的关系式,并讨论函数
满足的关系式,并讨论函数![]() 的单调区间;
的单调区间;
(2)已知![]() ,若函数
,若函数![]() 在
在![]() 上有且只有一个零点,求实数
上有且只有一个零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
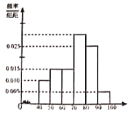
【题目】曙光中学团委组织了“弘扬奥运精神,爱我中华”的知识竞赛,从参加考试的学生中抽出![]() 名学生,将其成绩(均为整数)分成六段
名学生,将其成绩(均为整数)分成六段![]() ,
,![]() ,
,![]() ,
,![]() 后画出如下部分频率分布直方图,则第四小组的频率为_______,从成绩是
后画出如下部分频率分布直方图,则第四小组的频率为_______,从成绩是![]() 和
和![]() 的学生中选两人,他们在同一分数段的概率_______.
的学生中选两人,他们在同一分数段的概率_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从8名运动员中选4人参加![]() 米接力赛,在下列条件下,各有多少种不同的排法?
米接力赛,在下列条件下,各有多少种不同的排法?
(1)甲、乙两人必须入选且跑中间两棒;
(2)若甲、乙两人只有一人被选且不能跑中间两棒;
(3)若甲、乙两人都被选且必须跑相邻两棒;
(4)甲不在第一棒.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 为边
为边![]() 的中点.将△
的中点.将△![]() 沿
沿![]() 翻折,得到四棱锥
翻折,得到四棱锥![]() .设线段
.设线段![]() 的中点为
的中点为![]() ,在翻折过程中,有下列三个命题:
,在翻折过程中,有下列三个命题:
① 总有![]() 平面
平面![]() ;
;
② 三棱锥![]() 体积的最大值为
体积的最大值为![]() ;
;
③ 存在某个位置,使![]() 与
与![]() 所成的角为
所成的角为![]() .
.
其中正确的命题是____.(写出所有正确命题的序号)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com