
����Ŀ��ij����2014����2019��ÿ�����ͳ�����õ��˿��������±���ʾ:
��� | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
����/ǧ�� | 2082 | 2135 | 2203 | 2276 | 2339 | 2385 |
(1)���ݱ��е����ݼ���2014����2018��ÿ��õ��˿ڵ���������,�������õ��˿������ı仯���ƣ�
(2)�о���Ա�ú���![]() ��ϸõص��˿�����,����
��ϸõص��˿�����,����![]() �ĵ�λ����,2014�����Ӧʱ��
�ĵ�λ����,2014�����Ӧʱ��![]() �ĵ�λ�Ǹ��ˣ���
�ĵ�λ�Ǹ��ˣ���![]() �ķ�����Ϊ
�ķ�����Ϊ![]() ��
��![]() ��ֵ(��ȷ��0.1),��������ʵ������.
��ֵ(��ȷ��0.1),��������ʵ������.
���𰸡���1������������2��T��2400����5.5��������.
��������
��1�����ݱ��е����ݿɵô�2014�굽2019�˺����ӵ��������������࣬��2017�����ӵ�����������٣����˿����������������ӵģ�
��2�����ݺ����ı���ʽ���Լ��������Ķ��壬��ֵ���㼴�ɣ�
�⣺��1��2014����2019��ÿ��õ��˿ڵ���������Ϊ2385��2082��303ǧ�ˣ�
3135��2082��53��2203��2135��68��2276��2203��73��2339��2276��63��2385��2339��46��
���������ݿɵô�2014�굽2019��ÿ���˿����������������Ӻ���ٵı仯���ƣ�ÿһ���˿������������ı仯���ƣ�
��2����![]() ��
��
��P��t���ķ�����ΪT��x����
��2400��2000![]() ��
��
��4.4878e��0.6554t+1![]() ��
��
��4.4878e��0.6554t![]() ��
��
����ȡ�����ɵ�ln4.4878��0.6554t����ln8��
��t![]() 5.5��
5.5��
��T��2400����5.5��
��ʵ������Ϊ���ɸ�����ѧģ��Ԥ���˿������������ɣ����ṩ��Ч���ݣ�����������ʱ�䣬�õ��˿�����������������2400ǧ�ˣ�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ������
������![]() ���Һ�ֱ��
���Һ�ֱ��![]() ����.
����.
(��)��ö�ԲԲ��![]() �Ĺ켣
�Ĺ켣![]() �ķ��̣�
�ķ��̣�
(��)��֪��![]() ����б��Ϊ1��ֱ��
����б��Ϊ1��ֱ��![]() ���߶�
���߶�![]() �ཻ������������ԭ��
�ཻ������������ԭ��![]() �͵�
�͵�![]() ������������
������������![]() ����
����![]() ���㣬��
���㣬��![]() ��������ֵ.
��������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ֱ������![]() �У�
��![]() ��
��![]() ����
����![]() ��
��![]() �ϣ���
�ϣ���![]() ����
����![]() ��
��![]() ����ʹ��ƽ��
����ʹ��ƽ��![]() ƽ��
ƽ��![]() (��ͼ2).
(��ͼ2).![]() Ϊ
Ϊ![]() �е�
�е�
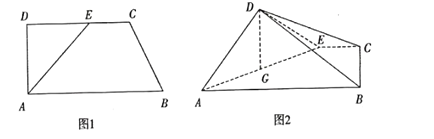
(1)��֤:![]() ��
��
(2)������![]() �������
�������
(3)���߶�![]() ���Ƿ���ڵ�
���Ƿ���ڵ�![]() ��ʹ��
��ʹ��![]() ƽ��
ƽ��![]() �������ڣ���
�������ڣ���![]() ��ֵ���������ڣ���˵������
��ֵ���������ڣ���˵������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() �У�ƽ��
�У�ƽ��![]() ƽ��
ƽ��![]() ��
��![]() Ϊ�ȱ������Σ�
Ϊ�ȱ������Σ�![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() ���е㣮
���е㣮
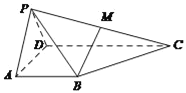
��1����֤��![]() ƽ��PAD��
ƽ��PAD��
��2��������P��BC��D������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ʹ���ǵ����������ݣ���������Ҳ��ʼ��Ϊ�������ճ������в��ɻ�ȱ��һ���֣�ij��һ���������Ը����г�ռ���ʽϸߵļס�����������������ҵ�����������ס������ң��ľ�Ӫ��������˵��飬���������±���
1�� | 2�� | 3�� | 4�� | 5�� | |
�������սӵ�x���ٵ��� | 5 | 2 | 9 | 8 | 11 |
�������սӵ�y���ٵ��� | 2 | 3 | 10 | 5 | 15 |
��1���Ը��ݱ�������������սӵ����������ͳ�ƵĽǶ�˵��������������ҵ�ľ�Ӫ״����
��2����ͳ�Ʊ�����y��x֮��������Թ�ϵ.
���������ϵ��r��y��x֮��������ǿ�������жϣ�����![]() �������Ϊy��x�н�ǿ��������ع�ϵ��rֵ��ȷ��0.001����
�������Ϊy��x�н�ǿ��������ع�ϵ��rֵ��ȷ��0.001����
�ھ��������y��x֮��Ļع鷽��Ϊ![]() ���ٶ�ÿ������ҵ����ҵƽ���ܻ�����3Ԫ����Ԥ��������սӵ���������25�ٵ�ʱ������������ȡ���մ�����Ĵ��·�Χ.��xֵ��ȷ��0.01��
���ٶ�ÿ������ҵ����ҵƽ���ܻ�����3Ԫ����Ԥ��������սӵ���������25�ٵ�ʱ������������ȡ���մ�����Ĵ��·�Χ.��xֵ��ȷ��0.01��
��ع�ʽ��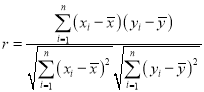 ��
��
�ο����ݣ�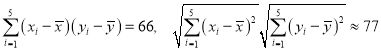 .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() �ڽ�����O��
�ڽ�����O��![]() ƽ��ABC��
ƽ��ABC��![]() Ϊ�ȱ������Σ��ұ߳�
Ϊ�ȱ������Σ��ұ߳�![]() ����
����![]() �ı����Ϊ
�ı����Ϊ![]() ����ֱ��PC��ƽ��PAB���ɵĽǵ�����ֵΪ
����ֱ��PC��ƽ��PAB���ɵĽǵ�����ֵΪ
A.![]() B.
B.![]()
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��
�������ں���![]() �Ķ������ڴ�������
�Ķ������ڴ�������![]() ��ʹ�øú���������
��ʹ�øú���������![]() ��Ϊ����������ʵ��
��Ϊ����������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
����![]() ʱ��������
ʱ��������![]() �ڵ�
�ڵ�![]() ��������
��������![]() ������
������![]() ����ֻ��һ�������㣬��ʵ��
����ֻ��һ�������㣬��ʵ��![]() ��ֵ��ȡֵ��Χ��
��ֵ��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���![]() �У�
��![]() ��
��![]() ��
��![]() ��
Ϊ��![]() ���е㣮����
���е㣮����![]() ��
��![]() ���ۣ��õ�����
���ۣ��õ�����![]() �����߶�
�����߶�![]() ���е�Ϊ
���е�Ϊ![]() ���ڷ��۹����У��������������⣺
���ڷ��۹����У��������������⣺
�� ����![]() ƽ��
ƽ��![]() ��
��
�� ����![]() ��������ֵΪ
��������ֵΪ![]() ��
��
�� ����ij��λ�ã�ʹ![]() ��
��![]() ���ɵĽ�Ϊ
���ɵĽ�Ϊ![]() ��
��
������ȷ��������____����д��������ȷ�������ţ�

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com