
分析 (1)判断直线经过圆的圆心,然后求解弦长.
(2)弦AB被点P平分时,AB⊥PC,kAB•kPC=-1,又kPC=-1,然后求解直线方程.
(3)设M(x0,y0),则满足${x_0}^2+{y_0}^2+2{x_0}-3=0$,①,通过$\frac{|MO|}{|MR|}=λ$,即$\frac{{\sqrt{{x_0}^2+{y_0}^2}}}{{\sqrt{{{({x_0}-a)}^2}+{y_0}^2}}}=λ$.然后求解即可.
解答 解:(1)由题意知,圆心C(1,0),半径R=2,直线AB的方程为x+y+1=0,
直线AB过圆心C,所以弦长AB=2R=4.…(4分)
(2)当弦AB被点P平分时,AB⊥PC,kAB•kPC=-1,又kPC=-1,
所以kAB=1,直线AB的方程为x-y+3=0.…(8分)
(3)设M(x0,y0),则满足${x_0}^2+{y_0}^2+2{x_0}-3=0$,①…(9分)
由题意得,$\frac{|MO|}{|MR|}=λ$,即$\frac{{\sqrt{{x_0}^2+{y_0}^2}}}{{\sqrt{{{({x_0}-a)}^2}+{y_0}^2}}}=λ$.…(10分)
整理得${x_0}^2+{y_0}^2={λ^2}[{x_0}^2-2a{x_0}+{a^2}+{y_0}^2]$,②
由①②得,$3-2{x_0}={λ^2}[3-2{x_0}-2a{x_0}+{a^2}]$恒成立,
所以$\left\{\begin{array}{l}3={λ^2}(3+{a^2})\\-2={λ^2}(-2-2a)\end{array}\right.$,又a≠0,λ>0,λ≠1,
解之得a=3.…(12分)
点评 本题考查直线与圆的位置关系的综合应用,考查转化思想以及计算能力.


科目:高中数学 来源: 题型:选择题
| A. | {-3,-4} | B. | {-1,-2} | C. | {0} | D. | ∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若两条直线和同一个平面所成的角相等,则这两条直线平行 | |
| B. | 若一个平面内有三个点到另一个平面的距离相等,则这两个平面平行 | |
| C. | 若一条直线和两个相交平面都平行,则这两条直线与这两个平面的交线平行 | |
| D. | 若两个平面都垂直于第三个平面,则这两个平面平行 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
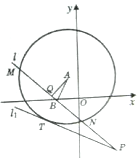 已知以A(-1,2)点为圆心的圆与直线${l_1}:\frac{1}{2}x+y+\frac{7}{2}=0$相切.过点B(-2,0)的动直线l与圆A相交于M,N两点,Q是MN的中点,直线l与l1相交于点P.
已知以A(-1,2)点为圆心的圆与直线${l_1}:\frac{1}{2}x+y+\frac{7}{2}=0$相切.过点B(-2,0)的动直线l与圆A相交于M,N两点,Q是MN的中点,直线l与l1相交于点P.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com