
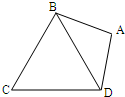
 如图,在平面四边形ABCD中,AB=AD=1,∠BAD=θ,而△BCD是正三角形,
如图,在平面四边形ABCD中,AB=AD=1,∠BAD=θ,而△BCD是正三角形, AB•AD•sinA=
AB•AD•sinA= ×1×1×sinθ=
×1×1×sinθ= sinθ,
sinθ, BD2,
BD2, sinθ+
sinθ+ (2-2cosθ),
(2-2cosθ), +sin(θ-
+sin(θ- )其中0<θ<π;
)其中0<θ<π; +sin(θ-
+sin(θ- ),
), <θ-
<θ- <
< ,
, =
= 时,S取得最大值1+
时,S取得最大值1+ ,此时θ=
,此时θ= +
+ =
= .
. BD2,接着由AB,AD及cosA的值,利用余弦定理表示出BD2,可表示出三角形BCD的面积,两者相加去括号后,利用两角和与差的正弦函数公式化简可表示出四边形ABCD的面积,并求出此时θ的范围;
BD2,接着由AB,AD及cosA的值,利用余弦定理表示出BD2,可表示出三角形BCD的面积,两者相加去括号后,利用两角和与差的正弦函数公式化简可表示出四边形ABCD的面积,并求出此时θ的范围;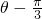 的范围,再由正弦函数的图象与性质可得出面积S的最大值,以及此时θ的度数.
的范围,再由正弦函数的图象与性质可得出面积S的最大值,以及此时θ的度数.

科目:高中数学 来源: 题型:
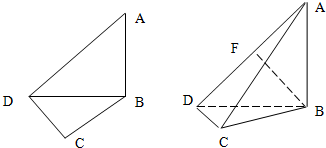
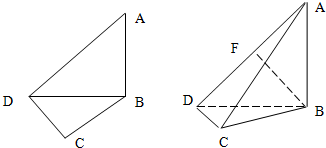 如图,在平面四边形ABCD中,已知∠A=45°,∠C=90°,∠ADC=105°,AB=BD,现将四边形ABCD沿BD折起,使平面ABD⊥平面BDC,设点F为棱AD的中点.
如图,在平面四边形ABCD中,已知∠A=45°,∠C=90°,∠ADC=105°,AB=BD,现将四边形ABCD沿BD折起,使平面ABD⊥平面BDC,设点F为棱AD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
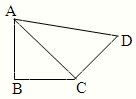 如图,在平面四边形ABCD中,AB=BC=CD=a,∠ABC=90°,∠BCD=135°,沿对角线AC将此四边形折成直二面角.
如图,在平面四边形ABCD中,AB=BC=CD=a,∠ABC=90°,∠BCD=135°,沿对角线AC将此四边形折成直二面角.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
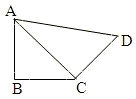 如图,在平面四边形ABCD中,AB=BC=CD=a,∠ABC=90°,∠BCD=135°,沿对角线AC将此四边形折成直二面角.
如图,在平面四边形ABCD中,AB=BC=CD=a,∠ABC=90°,∠BCD=135°,沿对角线AC将此四边形折成直二面角.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com