
 ,且其图象关于直线x=0对称,则( )
,且其图象关于直线x=0对称,则( ) 上为增函数
上为增函数 上为减函数
上为减函数 ,且在
,且在 上为增函数
上为增函数 ,且在
,且在 上为减函数
上为减函数 ](k∈Z),可得出(0,
](k∈Z),可得出(0, )?[kπ,kπ+
)?[kπ,kπ+ ](k∈Z),即可得到函数在(0,
](k∈Z),即可得到函数在(0, )上为减函数,进而得到正确的选项.
)上为减函数,进而得到正确的选项. cos(2x+φ)+sin(2x+φ)
cos(2x+φ)+sin(2x+φ) cos(2x+φ)+
cos(2x+φ)+ sin(2x+φ)]
sin(2x+φ)] ),
), =π,
=π, =kπ(k∈Z),即φ=kπ+
=kπ(k∈Z),即φ=kπ+ (k∈Z),
(k∈Z), ,
, ,
, (k∈Z),
(k∈Z), ](k∈Z),
](k∈Z), )?[kπ,kπ+
)?[kπ,kπ+ ](k∈Z),
](k∈Z), )上为减函数,
)上为减函数, )上为减函数.
)上为减函数.

 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案科目:高中数学 来源:2012-2013学年山西省太原五中高三(上)12月月考数学试卷(文科)(解析版) 题型:选择题
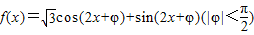 ,且其图象关于直线x=0对称,则( )
,且其图象关于直线x=0对称,则( )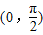 上为增函数
上为增函数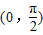 上为减函数
上为减函数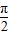 ,且在
,且在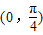 上为增函数
上为增函数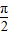 ,且在
,且在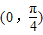 上为减函数
上为减函数查看答案和解析>>
科目:高中数学 来源:2012年河北省普通高中高考数学模拟试卷(理科)(解析版) 题型:选择题
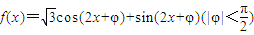 ,且其图象关于直线x=0对称,则( )
,且其图象关于直线x=0对称,则( )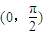 上为增函数
上为增函数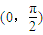 上为减函数
上为减函数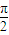 ,且在
,且在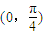 上为增函数
上为增函数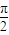 ,且在
,且在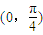 上为减函数
上为减函数查看答案和解析>>
科目:高中数学 来源:2011-2012学年甘肃省天水一中、甘谷一中高三(下)第八次联考数学试卷(解析版) 题型:选择题
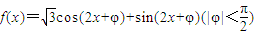 ,且其图象关于直线x=0对称,则( )
,且其图象关于直线x=0对称,则( )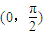 上为增函数
上为增函数 上为减函数
上为减函数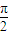 ,且在
,且在 上为增函数
上为增函数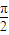 ,且在
,且在 上为减函数
上为减函数查看答案和解析>>
科目:高中数学 来源:2013届山西省高三12月月考文科数学试卷(解析版) 题型:选择题
设函数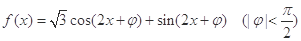 ,且其图象关于直线
,且其图象关于直线
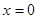 对称,则( )
对称,则( )
A.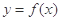 的最小正周期为
的最小正周期为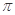 ,且在
,且在 上为增函数
上为增函数
B.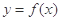 的最小正周期为
的最小正周期为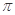 ,且在
,且在 上为减函数
上为减函数
C.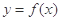 的最小正周期为
的最小正周期为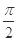 ,且在
,且在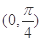 上为增函数
上为增函数
D.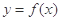 的最小正周期为
的最小正周期为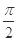 ,且在
,且在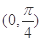 上为减函数
上为减函数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com