
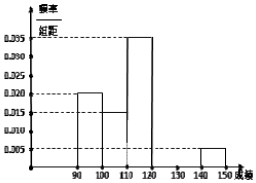
 某校高三数学竞赛初赛考试结束后,对考生成绩进行统计(考生成绩均不低于90分,满分150分),将成绩按如下方式分为六组,第一组.如图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人.
某校高三数学竞赛初赛考试结束后,对考生成绩进行统计(考生成绩均不低于90分,满分150分),将成绩按如下方式分为六组,第一组.如图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人.分析 (1)利用频率分布直方图的性质即可得出.
(2)依题意可得:第四组人数为:$4×\frac{0.015}{0.005}$=12,可得P1=$\frac{{∁}_{12}^{1}{∁}_{4}^{1}}{{∁}_{16}^{2}}$.
(3)依题意可得:样本总人数为:$\frac{4}{0.05}$=80,成绩不低于120分的人数为:80×(0.05+0.10+0.15)=24,故在样本中任选1人,其成绩不低于120分的概率=$\frac{24}{80}$=$\frac{3}{10}$.由已知ξ的可能取值为0,1,2,3.ξ~B$(3,\frac{3}{10})$,即可得出.
解答 解:(1)频率分布直方图见解析,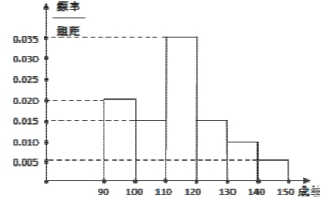
M=95×0.2+105×0.15+115×0.35+125×0.15+135×0.1+145×0.05=114.5;
(2)依题意可得:第四组人数为:
$4×\frac{0.015}{0.005}$=12,
故P1=$\frac{{∁}_{12}^{1}{∁}_{4}^{1}}{{∁}_{16}^{2}}$=$\frac{2}{5}$;
(3)依题意可得:样本总人数为:$\frac{4}{0.05}$=80,成绩不低于120分的人数为:80×(0.05+0.10+0.15)=24,故在样本中任选1人,其成绩不低于120分的概率=$\frac{24}{80}$=$\frac{3}{10}$.由已知ξ的可能取值为0,1,2,3.
ξ~B$(3,\frac{3}{10})$,P(ξ=0)=$(1-\frac{3}{10})^{3}$=$\frac{343}{1000}$,P(ξ=1)=${∁}_{3}^{1}(1-\frac{3}{10})^{2}×\frac{3}{10}$=$\frac{441}{1000}$,
P(ξ=2)=${∁}_{3}^{2}(1-\frac{3}{10})×(\frac{3}{10})^{2}$=$\frac{189}{1000}$,
P(ξ=3)=$(\frac{3}{10})^{3}$=$\frac{27}{1000}$.ξ的分布列如下
| ξ | 0 | 1 | 2 | 3 |
| P | $\frac{343}{1000}$ | $\frac{441}{1000}$ | $\frac{189}{1000}$ | $\frac{27}{1000}$ |
点评 本题考查了频率分布直方图的性质、二项分布列的计算公式及其数学期望计算公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | (2,+∞) | B. | (1,+∞) | C. | (-∞,-2) | D. | (-∞,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com