
【题目】已知椭圆![]() (
(![]() )的离心率为
)的离心率为![]() ,连接椭圆四个顶点得到的菱形的面积为4.
,连接椭圆四个顶点得到的菱形的面积为4.
(1)求椭圆的方程;
(2)设![]() 是椭圆的右顶点,过点
是椭圆的右顶点,过点![]() 作两条互相垂直的直线
作两条互相垂直的直线![]() ,
,![]() 分别与椭圆交于
分别与椭圆交于![]() ,
,![]() 两点,求证:直线
两点,求证:直线![]() 过定点;
过定点;
(3)(只理科做)过点![]() 作两条互相垂直的直线
作两条互相垂直的直线![]() ,
,![]() ,
,![]() 与圆
与圆![]() :
:![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 交椭圆于另一点
交椭圆于另一点![]() ,求
,求![]() 面积的最大值.
面积的最大值.
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案科目:高中数学 来源: 题型:
【题目】某研究性学习小组对春季昼夜温差大小与某花卉种子发芽多少之间的关系进行研究,他们分别记录了3月1日至3月5日的每天昼夜温差与实验室每天每100颗种子浸泡后的发芽数,得到如下资料:
日期 | 3月1日 | 3月2日 | 3月3日 | 3月4日 | 3月5日 |
温差 | 10 | 11 | 13 | 12 | 8 |
发芽数 | 23 | 25 | 30 | 26 | 16 |
(1)求这5天的平均发芽率;
(2)从3月1日至3月5日中任选2天,记发芽的种子数分别为![]() ,
,![]() ,用
,用![]() 的形式列出所有的基本事件,并求满足
的形式列出所有的基本事件,并求满足![]() 的事件
的事件![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】养路处建造圆锥形无底仓库用于贮藏食盐(供融化高速公路上的积雪之用),已建的仓库的底面直径为12m,高4m,养路处拟建一个更大的圆锥形仓库,以存放更多食盐,现有两种方案:一是新建的仓库的底面直径比原来大4m(高不变);二是高度增加4m(底面直径不变).
(1)分别计算按这两种方案所建的仓库的体积;
(2)分别计算按这两种方案所建的仓库的表面积;
(3)哪个方案更经济些?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某医院治疗白血病有甲、乙两套方案,现就70名患者治疗后复发的情况进行了统计,得到其等高条形图如图所示(其中采用甲、乙两种治疗方案的患者人数之比为![]() .
.
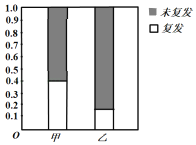
(1)补充完整![]() 列联表中的数据,并判断是否有
列联表中的数据,并判断是否有![]() 把握认为甲乙两套治疗方案对患者白血病复发有影响;
把握认为甲乙两套治疗方案对患者白血病复发有影响;
复发 | 未复发 | 总计 | |
甲方案 | |||
乙方案 | 2 | ||
总计 | 70 |
(2)为改进“甲方案”,按分层抽样组成了由5名患者构成的样本,求随机抽取2名患者恰好是复发患者和未复发患者各1名的概率.
附:
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 |
![]() ,
,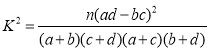 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设F是椭圆C:![]() (a>b>0)的一个焦点,P是椭圆C上的点,圆x2+y2=
(a>b>0)的一个焦点,P是椭圆C上的点,圆x2+y2=![]() 与线段PF交于A,B两点,若A,B三等分线段PF,则椭圆C的离心率为( )
与线段PF交于A,B两点,若A,B三等分线段PF,则椭圆C的离心率为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形ADEF与梯形ABCD所在的平面互相垂直,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.
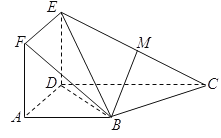
(1)求证:BM∥平面ADEF;
(2)求证:平面BDE⊥平面BEC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区有小学21所,中学14所,大学7所,现采取分层抽样的方法从这些学校中抽取6所学校对学生进行视力调查。
(I)求应从小学、中学、大学中分别抽取的学校数目。
(II)若从抽取的6所学校中随机抽取2所学校做进一步数据分析,
(1)列出所有可能的抽取结果;
(2)求抽取的2所学校均为小学的概率。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com