练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知θ是△ABC在平面内一定点，动点P满足
    OP
    =
    OA
    +λ(
    AB
    |
    AB
    |cosB
    +
    AC
    |
    AC
    |cosC
    )    ，λ∈（0，+∞），则动点P的轨迹一定通过△ABC的（　　）
    分析：可先根据数量积为零得出
    BC
    与λ（
    AB
    |
    AB
    | cosB
    +
    AC
    |
    AC
    | cosC
    ）垂直，可得点P在BC的高线上，从而得到结论．
    解答：解：∵
    OP
    =
    OA
    +λ(
    AB
    |
    AB
    |cos∠B
    +
    AC
    |
    AC
    |cos∠C
    )
    ∴
    OP
    -
    OA
    =λ(
    AB
    |
    AB
    |cos∠B
    +
    AC
    |
    AC
    |cos∠C
    )
    即
    AP
    =λ(
    AB
    |
    AB
    |cos∠B
    +
    AC
    |
    AC
    |cos∠C
    )    ．
    又∵
    BC
    •（
    AB
    |
    AB
    | cosB
    +
    AC
    |
    AC
    | cosC
    ）=-|
    BC
    |+|
    BC
    |=0
    ∴
    BC
    与λ（
    AB
    |
    AB
    | cosB
    +
    AC
    |
    AC
    | cosC
    ）垂直，
    即
    AP
    ⊥
    BC
    ，
    ∴点P在BC的高线上，即P的轨迹过△ABC的垂心
    故选B．
    点评：本题主要考查了向量在几何中的应用、空间向量的加减法、轨迹方程、以及三角形的五心等知识，解答关键是得出出
    BC
    与λ（
    AB
    |
    AB
    | cosB
    +
    AC
    |
    AC
    | cosC
    ）垂直，属于基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    16、给出下列四个命题：
    ①已知集合A⊆{1，2，3，4}，且A中至少含有一个奇数，则这样的集合A有12个；
    ②任意的三角形ABC中，有cos2A＜cos2B的充要条件是A＞B；
    ③平面上n个圆最多将平面分成2n2-4n+4个部分；
    ④空间中直角在一个平面上的正投影可以是钝角；
    其中真命题的序号是
    ①②
    （要求写出所有真命题的序号）．

    查看答案和解析>>

    科目：高中数学 来源：2009年高考数学第二轮复习热点专题测试卷：极限导数和复数(含详解) 题型：013

    已知z1＝1－i，z2＝2＋2i，z3＝－3＋2i，若在复平面上z1，z2，z3对应点分别为A、B、C，则△ABC是

    [　　]

    A．等腰三角形

    B．等边三角形

    C．等腰直角三角形

    D．钝角三角形

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    给出下列四个命题：
    ①已知集合A⊆{1，2，3，4}，且A中至少含有一个奇数，则这样的集合A有12个；
    ②任意的三角形ABC中，有cos2A＜cos2B的充要条件是A＞B；
    ③平面上n个圆最多将平面分成2n2-4n+4个部分；
    ④空间中直角在一个平面上的正投影可以是钝角；
    其中真命题的序号是______（要求写出所有真命题的序号）．

    查看答案和解析>>

    科目：高中数学 来源：2009-2010学年山东省德州市鲁北中学高三（上）期末数学试卷（解析版） 题型：填空题

    给出下列四个命题：
    ①已知集合A⊆{1，2，3，4}，且A中至少含有一个奇数，则这样的集合A有12个；
    ②任意的三角形ABC中，有cos2A＜cos2B的充要条件是A＞B；
    ③平面上n个圆最多将平面分成2n2-4n+4个部分；
    ④空间中直角在一个平面上的正投影可以是钝角；
    其中真命题的序号是    （要求写出所有真命题的序号）．

    查看答案和解析>>

    科目：高中数学 来源：2010年浙江省嘉兴市高考数学一模试卷（理科）（解析版） 题型：选择题

    我们把底面是正三角形，顶点在底面的射影是正三角形中心的三棱锥称为正三棱锥、现有一正三棱锥P-ABC放置在平面上，已知它的底面边长为2，高h，边BC在平面上转动，若某个时刻它在平面上的射影是等腰直角三角形，则h的取值范围是（ ）

    A．（0，]
    B．（0，]
    C．（0，]∪[，1]
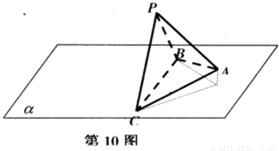
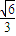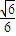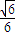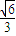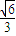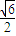    D．（0，]∪（，1）

    查看答案和解析>>

    同步练习册答案