
【题目】已知函数![]() ,若对任意
,若对任意![]() ,存在
,存在![]() ,使
,使![]() ,则实数b的取值范围是
,则实数b的取值范围是![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】∵函数f(x)![]() (x>0)
(x>0)
∴f′(x)![]()
若f′(x)>0,1<x<3,f(x)为增函数;若f′(x)<0,x>3或0<x<1,f(x)为减函数;
f(x)在x∈(0,2)上有极值,
f(x)在x=1处取极小值也是最小值f(x)min=f(1)=![]() ;
;
∵g(x)=x2﹣2bx+4=(x﹣b)2+4﹣b2,对称轴x=b,x∈[1,2],
当b<1时,g(x)在x=1处取最小值g(x)min=g(1)=1﹣2b=4=5﹣2b;
当1<b<2时,g(x)在x=b处取最小值g(x)min=g(b)=4﹣b2;
当b>2时,g(x)在[1,2]上是减函数,g(x)min=g(2)=4﹣4b+4=8﹣4b;
∵对任意x1∈(0,2),存在x2∈[1,2],使f(x1)≥g(x2),
∴只要f(x)的最小值大于等于g(x)的最小值即可,
当b<1时, ![]() ≥5﹣2b,解得b≥
≥5﹣2b,解得b≥![]() ,故b无解;当b>2时,
,故b无解;当b>2时, ![]() ≥8﹣4b,解得b≥
≥8﹣4b,解得b≥![]() ,
,
综上:b≥![]() ,
,
故答案为:C。


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 是
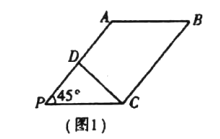
是![]() 中点(如图1).将
中点(如图1).将![]() 沿
沿![]() 折起到图2中
折起到图2中![]() 的位置,得到四棱锥
的位置,得到四棱锥![]() .
.
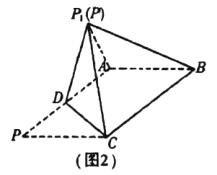
(1)将![]() 沿
沿![]() 折起的过程中,
折起的过程中, ![]() 平面
平面![]() 是否成立?并证明你的结论;
是否成立?并证明你的结论;
(2)若![]() 与平面
与平面![]() 所成的角为60°,且
所成的角为60°,且![]() 为锐角三角形,求平面
为锐角三角形,求平面![]() 和平面
和平面![]() 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.
(Ⅰ)求椭圆![]() 的方程.
的方程.
(Ⅱ)若![]() ,
, ![]() 是椭圆
是椭圆![]() 上两个不同的动点,且使
上两个不同的动点,且使![]() 的角平分线垂直于
的角平分线垂直于![]() 轴,试判断直线
轴,试判断直线![]() 的斜率是否为定值?若是,求出该值;若不是,说明理由.
的斜率是否为定值?若是,求出该值;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】按要求写出下列命题,并判断真假:
(1)命题:“在![]() 中,若
中,若![]() 则
则![]() ”的逆命题;
”的逆命题;
(2)命题:“若两个数的和为有理数,则这两个数都是有理数。”的否命题;
(3)命题:“若a≠0且b≠0,则ab≠0”的逆否命题;
(4)命题:“a=0或b=0,则a2+b2=0”的逆否命题;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 天气预报说明天下雨的概率为![]() ,则明天一定会下雨
,则明天一定会下雨
B. 不可能事件不是确定事件
C. 统计中用相关系数![]() 来衡量两个变量的线性关系的强弱,若
来衡量两个变量的线性关系的强弱,若![]() 则两个变量正相关很强
则两个变量正相关很强
D. 某种彩票的中奖率是![]() ,则买1000张这种彩票一定能中奖
,则买1000张这种彩票一定能中奖
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着资本市场的强势进入,互联网共享单车“忽如一夜春风来”,遍布了一二线城市的大街小巷.为了解共享单车在![]() 市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中随机抽取了200人进行抽样分析,得到下表(单位:人):
市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中随机抽取了200人进行抽样分析,得到下表(单位:人):
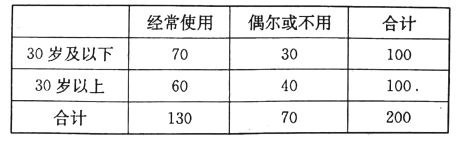
(Ⅰ)根据以上数据,能否在犯错误的概率不超过0.15的前提下认为![]() 市使用共享单车情况与年龄有关?(Ⅱ)①现从所抽取的30岁以上的网民中,按“经常使用”与“偶尔或不用”这两种类型进行分层抽样抽取10人,然后,再从这10人中随机选出3人赠送优惠券,求选出的3人中至少有2人经常使用共享单车的概率.
市使用共享单车情况与年龄有关?(Ⅱ)①现从所抽取的30岁以上的网民中,按“经常使用”与“偶尔或不用”这两种类型进行分层抽样抽取10人,然后,再从这10人中随机选出3人赠送优惠券,求选出的3人中至少有2人经常使用共享单车的概率.
②将频率视为概率,从![]() 市所有参与调查的网民中随机抽取10人赠送礼品,记其中经常使用共享单车的人数为
市所有参与调查的网民中随机抽取10人赠送礼品,记其中经常使用共享单车的人数为![]() ,求
,求![]() 的数学期望和方差.
的数学期望和方差.
参考公式:  ,其中
,其中![]() .
.
参考数据:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com