
【题目】某公司为了解广告投入对销售收益的影响,在若干地区各投入4万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示),由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从0开始计数的.
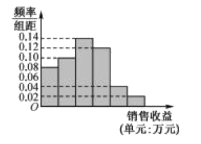
(1)根据频率分布直方图计算图中各小长方形的宽度;
(2)试估计该公司在若干地区各投入4万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);
(3)该公司按照类似的研究方法,测得另外一些数据,并整理得到下表:
广告投入 | 1 | 2 | 3 | 4 | 5 |
销售收益 | 2 | 3 | 3 | 7 |
由表中的数据显示,![]() 与
与![]() 之间存在着线性相关关系,请将(2)的结果填入空白栏,并求出
之间存在着线性相关关系,请将(2)的结果填入空白栏,并求出![]() 关于
关于![]() 的回归直线方程.(参考公式:
的回归直线方程.(参考公式: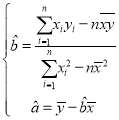 )
)
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:高中数学 来源: 题型:
【题目】某工厂的![]() ,
,![]() ,
,![]() 三个不同车间生产同一产品的数量(单位:件)如下表所示.质检人员用分层抽样的方法从这些产品中共抽取6件样品进行检测:
三个不同车间生产同一产品的数量(单位:件)如下表所示.质检人员用分层抽样的方法从这些产品中共抽取6件样品进行检测:
车间 |
|
|
|
数量 | 50 | 150 | 100 |
(1)求这6件样品中来自![]() ,
,![]() ,
,![]() 各车间产品的数量;
各车间产品的数量;
(2)若在这6件样品中随机抽取2件进行进一步检测,求这2件产品来自相同车间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 命题“若x2=1,则x≠1”的否命题是“若x2=1,则x=1”
B. 命题“![]() ”的否定是“x∈R,x2﹣x>0”
”的否定是“x∈R,x2﹣x>0”
C. “y=f(x)在x0处有极值”是“f'(x0)=0”的充要条件
D. 命题“若函数f(x)=x2﹣ax+1有零点,则“a≥2或a≤﹣2”的逆否命题为真命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,
中,![]() 平面ABCD,底面ABCD是正方形,
平面ABCD,底面ABCD是正方形,![]() ,E为PC上一点,当F为DC的中点时,EF平行于平面PAD.
,E为PC上一点,当F为DC的中点时,EF平行于平面PAD.
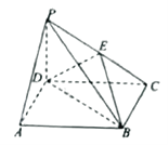
(Ⅰ)求证:![]() 平面PCB;
平面PCB;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】江苏省高邮市素有“鱼米之乡”之称,高邮城西有风光秀丽的高邮湖,湖内盛产花鲢鱼,记花鲢鱼在湖中的游速为![]() ,花鲢鱼在湖中的耗氧量的单位数为
,花鲢鱼在湖中的耗氧量的单位数为![]() ,经研究花鲢鱼的游速
,经研究花鲢鱼的游速![]() 与
与![]() 成正比,经测定,当花鲢鱼的耗氧量为200单位时,其游速为
成正比,经测定,当花鲢鱼的耗氧量为200单位时,其游速为![]() .
.
(1)求![]() 关于
关于![]() 的函数关系式
的函数关系式
(2)计算花鲢鱼静止时耗氧量的单位数.
(3)如果某条花鲢鱼的游速提高了1![]() ,那么它的耗氧量的单位数是原来的多少倍?
,那么它的耗氧量的单位数是原来的多少倍?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 的定义域为
的定义域为![]() ,对于区间
,对于区间![]() ,若
,若![]() 满足
满足![]() ,则称区间
,则称区间![]() 为函数
为函数![]() 的
的![]() 区间.
区间.
(1)证明:区间![]() 是函数
是函数![]() 的
的![]() 区间;
区间;
(2)若区间![]() 是函数
是函数![]() 的
的![]() 区间,求实数
区间,求实数![]() 的取值范围;
的取值范围;
(3)已知函数![]() 在区间
在区间![]() 上的图象连续不断,且在
上的图象连续不断,且在![]() 上仅有
上仅有![]() 个零点,证明:区间
个零点,证明:区间![]() 不是函数
不是函数![]() 的
的![]() 区间.
区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某颜料公司生产A,B两种产品,其中生产每吨A产品,需要甲染料1吨,乙染料4吨,丙染料2吨,生产每吨B产品,需要甲染料1吨,乙染料0吨,丙染料5吨,且该公司一天之内甲、乙、丙三种染料的用量分别不超过50吨,160吨和200吨,如果A产品的利润为300元/吨,B产品的利润为200元/吨,设公司计划一天内安排生产A产品x吨,B产品y吨.
(I)用x,y列出满足条件的数学关系式,并在下面的坐标系中画出相应的平面区域;
(II)该公司每天需生产A,B产品各多少吨可获得最大利润,最大利润是多少?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 经过点
经过点![]() .
.
(1)写出抛物线![]() 的标准方程及其准线方程,并求抛物线
的标准方程及其准线方程,并求抛物线![]() 的焦点到准线的距离;
的焦点到准线的距离;
(2)过点![]() 且斜率存在的直线
且斜率存在的直线![]() 与抛物线
与抛物线![]() 交于不同的两点
交于不同的两点![]() ,
,![]() ,且点
,且点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
(i)求点![]() 的坐标;
的坐标;
(ii)求![]() 与
与![]() 面积之和的最小值.
面积之和的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com